http://dev.gameres.com/Program/Visual/3D/bobic.htm
自从计算机游戏出现以来,程序员就不断地想办法来更精确地模拟现实世界。就拿乒乓游戏为例子(译者:Pong—被誉为电子游戏的祖先,有幸见过一次:),能见到祖先做的游戏感觉真是爽啊,想看的可以到FTP上下载“地球故事”就可以看到了:),游戏中有一个象征性的小方块(球)和两支拍子,游戏者需要在恰当的时间将拍子移动到恰当的地点,将小球反弹回去。这个基本操作的背后(以现在的标准来看)就是最原初的碰撞检测了。今天的游戏比“乒乓”要高级得多,并且基本上是基于3D的。3D游戏中的碰撞检测比“乒乓”游戏里的要更加难实现。玩一些早期模拟飞行游戏的体验向我们展现出糟糕的碰撞检测是如何毁灭一个游戏的。当穿过一座大山的尖顶的时候仍然活着,感觉很不真实。即便是现在的一些游戏也还是有碰撞上的问题,许多玩家曾经失望地看着他们喜爱的英雄或女英雄的部分身体穿进了墙里。甚至更糟的是,许多玩家都有过这样糟糕的体验,就是被那些离得很远的子弹或火箭击中。因为游戏者们要求提升真实性,我们开发者就不得不绞尽脑汁想办法让我们的游戏世界尽可能地接近现实世界。
阅读这篇文章前首先假设你对与碰撞检测相关的几何和数学知识已经有了基本的了解。在文章的最后,我将提供一些这方面的参考资料,以免你对它们感觉有点生疏。另外我还假设你已经读过 Jeff Lander 的图形专栏里关于碰撞检测文章(“Crashing into the New Year,” ; “When Two Hearts Collide,”;和 “Collision Response: Bouncy, Trouncy, Fun,”)。我将首先进行一个大概的描述,然后快速地切入到核心内容里,通过这两步从上至下地深入到碰撞检测中。我将讨论两种类型的图形引擎中的碰撞检测:基于 portal 的和基于 BSP 的。每种引擎中多边形的组织各不相同,因此在 world-object 型的碰撞检测上存在很大的差别。而object-object 型的碰撞检测绝大多数地方在上述两种引擎里的是一样的,主要看你是如何实现的了。当我们接触到多边形的碰撞检测时,我们还会实验如何将其扩展到我们学过的凸型物体上。
预览
为了创建一个理想的碰撞检测程序,我们不得不在开发一个游戏的的图形管道的同时就开始计划并创建它的框架。在项目的最后加入碰撞检测是相当困难的。想在开发周期的末尾创建快速的碰撞检测将很有可能会使整个游戏被毁掉,因为我们不可能使它能高效地运行。在好的游戏引擎中,碰撞检测应该是精确、有效并且十分快速的。这些要求意味着碰撞检测将要与场景的多边形管理管道紧紧地联系起来。这也意味着穷举法将无法工作――今天的3D游戏中每帧处理的数据量很可能导致打格,当你还在检测一个物体的各多边形是否与场景中的其它多边形碰撞时,时间已经过去了。
让我们从基本的游戏引擎循环开始吧(列表1)。快速浏览这些代码来得到碰撞检测的相关策略。我们先假设碰撞没有发生,然后更新物体的位置,如果发现发生了碰撞,我们将把物体移回原来的位置不允许它穿越边界(或将物体销毁或执行一些预防措施)。然而,这个假设太过简单因为我们无法得知物体原来的位置是否仍然有效。你必须为这种情况设计一个方案(否则你可能会体验到坠机或被子弹击中的感觉――就是前面举的例子)。如果你是一个热心的玩家,你可能已经注意到了在一些游戏当中,当你挨着墙壁并试图穿过去的时候,摄像机就开始震动。你正经历的就是将主角移回原位的情况。震动是因为取了较大的时间片引起的。
Listing 1. Extremely Simplified Game Loop
while(1){
process_input();
update_objects();
render_world();
}
update_objects(){
for (each_object)
save_old_position();
calc new_object_position
{based on velocity accel. etc.}
if (collide_with_other_objects())
new_object_position = old_position();
{or if destroyed object remove it etc.}
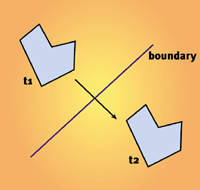
Figure 1. Time gradient and collision tests.
但是我们的方法有缺陷,我们忘了在等式中加入时间。图1告诉我们时间太重要了不能忘了它。即便物体在 t1 或 t2 时刻没有发生碰撞,它仍有可能在 t 时刻穿过边界(t1<t<t2)。这会在两个连续帧中产生大幅度地跨越(就好象击中了燃料室或其它类似的东西)。我们不得不找一个好的方法来解决这个问题。
我们可以把时间看成是第四维并将所有运算在4维空间中进行。然而这可能会让运算变得十分复杂,所以我们会避开这些。我们还可以创建一个以 t1、t2时刻的物体为起始点的实心体,然后用它来与墙进行测试(见图2)
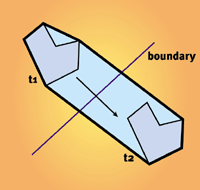
Figure 2. Solid created from the space that an object spans over a given time frame.
一个简单的方法就是创建一个凸壳来罩住两个不同时刻的物体。这种方法效率低下可能会明显地降低你的游戏速度。以其创建一个凸壳,还不如创建一个围绕实心体的包围盒。我们学习其它的技术后再回来讨论这个问题。
有另一种比较容易执行但精度较低的方法,就是把给定的时间段分为两分,然后测试时间中点的相交关系。我们还可以递归地依次测定各段的时间中点。这个方法比先前的方法要快得多,但不能保证能捕捉到所有的碰撞情况。
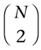
另一个暗藏着的问题是collide_with_other_objects()方法的实现――即判断一个物体是否与场景中的其它物体相交。如果场景中有很多的物体,这个方法可能消耗很大。如果要判断各物体与场景中其它物体是否相交,我们将不得不进行大概N选2次比较。因此比较次数会是N的平方次冪(或表示成O(N2))。但我们可以用几种方法来避免进行O(N2)对的比较。举个例子,我们可以把场景中的物体分成静态的(被撞物)和动态的(碰撞物――即使它的速度为0也行)。就好象房间中的墙壁是被撞物,而一个扔向墙壁的小球是碰撞物。我们可以创建两棵独立的树(每一棵对应一类物体),然后测试那些物体可能会碰撞的树。我们甚至可以对环境进行约定让一些碰撞物之间不发生碰撞――比如我们不需要在两颗子弹之间进行判断。现在在继续之前,(经过改进之后)我们可以说处理过程变得更加清晰了。(另一个减少场景中成对的比较的方法就是建立八叉树。这已经超出了这篇文章的范围,你可以在Spatial Data Structures: Quadtree, Octrees and Other Hierarchical Methods文章中的For Further Info一节里读到更多关于八叉的信息)。现在让我们来看一下基于 Portal 引擎,了解为什么在这类引擎中一提到碰撞检测就会那么痛苦。
Portal引擎和Object-Object型碰撞
基于 Portal 的引擎把场景或世界分割成较小的凸方形区域。凸方形区域很适合图形管道因为它们能避免重绘现象。不幸的是,对碰撞检测来说,凸方形区域会给我们带来一些困难。在我最近的一些测试中,一个引擎中平均大约有400到500个凸方形区域。当然,这个数字会随着不同的引擎而有所变化,因为不同的引擎使用不同的多边形技术。而且多边形的数目也会因场景的大小而有所不同。
判断一个物体的多边形是否穿过了场景中的多边形产生的运算量可能会很大。一个最简单的碰撞检测法就是用球形来近似地表示物体或物体的一部分,然后再判断这些包围球是否相交。这样我们仅仅需要测试两个球体中心的距离是否小于它们的半径合(这表示发生了碰撞)。如果我们是用中心点距离的平方和半径合的平方进行比较,那更好,这样我们可以在计算距离时除去拙劣的开方运算。但是,简单的运算也导致了精确度的降低(见图3)。

Figure 3. In a sphere-sphere intersection, the routine may report that collision has occurred when it really hasn’t.
但我们仅仅是将这个不太精确的方法做为我们的第一步。我们用一个大的球体代表整个对象,然后检测它是否和其它的球体相交。如果检测到发生了碰撞,那么我们就要进一步提高精度,我们可以将大的球体分割成一系列小的球体,并检查与各小球体是否发生碰撞。我们不断地分割检查直到得到满意的近似值为止。分层并分割的基本思想就是我们要尽可能达到适合需要的理想的情况。
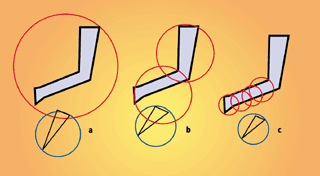
Figure 4. Sphere subdivision.
用球体去近似地代表物体运算量很小,但在游戏中的大多数物体是方的,我们应该用方盒来代表物体。开发者一直用包围盒和这种递归的快速方法来加速光线追踪算法。在实际中,这些算法已经以八叉和AABB(axis-aligned bounding boxes)的方式出现了。图5展示了一个AABB和它里面的物体。
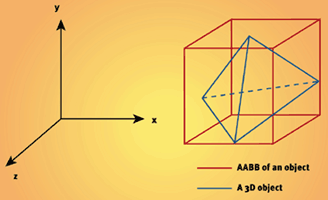
Figure 5. An object and its AABB.
坐标轴平行(“Axis-aligned”)不仅指盒体与世界坐标轴平行,同时也指盒体的每个面都和一条坐标轴垂直。这样一个基本信息就能减少转换盒体时操作的次数。AABBs 在当今的许多游戏中都得到了应用,开发者经常用它们作为模型的包围盒。再次指出,提高精度的同时也会降低速度。因为 AABBs 总是与坐标思平行,我们不能在旋转物体的时候简单地旋转 AABBs --- 它们应该在每一帧都重新计算过。如果我们知道每个对象的内容,这个计算就不算困难并不会降低游戏的速度。 然而,我们还面临着精度的问题。假如我们有一个3D的细长刚性直棒,并且要在每一帧动画中都重建它的AABB。我们可以看到每一帧中的包围盒的都不一样而且精度也会随之改变。
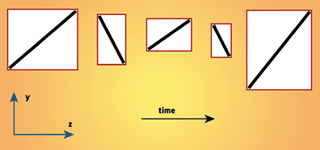
Figure 6. Successive AABBs for a spinning
rod (as viewed from the side).
所以以其用 AABBs,为什么我们不用任意方向能最小化空白区域的包围盒呢。这是一种基于叫 oriented bounding boxes—OBBs 的技术,它已经广泛用于光线追踪和碰撞检测中。这种技术不但比 AABBs 技术更精确而且还更健壮。但 OBBs 实现起来比较困难,执行速度慢,并且不太适合动态的或柔性的物体。特别注意的是当我们把一个物体分得越来越小的时候,我们事实上在创建一棵有层次的树。
我们是选择 AABBs 还是选择 OBBs 应该根据我们所需的精确程度而定。对一个需要快速反应的3D射击游戏来说,我们可能用 AABB 来进行碰撞检测更好些――我们可以牺牲一些精度来换取速度和实现的简单化。这篇文章附带的代码已经传到 Game Developer 网页上了。里面是从 AABBs 开始讲起,同时还提供了一些实现 OBBs 的碰撞检测包里的代码例子。好了,现在我们已经有了关于每一部分是如果工作的认识了,下面我们来看看实现的细节。
创建树
为任意的网格模型创建 OBB 树可能是算法里最难的一个部分,而且它还要调整以适合特定的引擎或游戏类型。图7示出了从最初的模型创建一个OBB树的整个过程。可以看到,我们不得不找出包围给定模型的最近似的包围盒(或者其它3D体)。
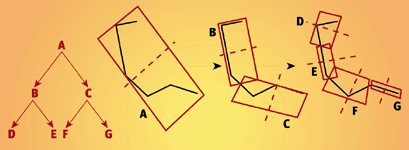
Figure 7. Recursive build of an OBB and its tree.
有几种方法可以事先计算OBB,这其中包括了许多的数学运算。其中一个基本的方法是计算顶点分布的均值,将它作为包围盒的中心,然后计算协方差矩阵。然后我们用协方差矩阵的三个特征向量中的两个把多边形和包围盒结合起来。我们可以凸盒方法进一步加速和优化树的创建。你可以在Gottschalk, Lin, 和 Manocha的文章中的“For Further Info”一节找到相关信息。建立AABB树要简单得多,因为我们不需要找出物体的最小的包围体和它们的轴。我们只需决定在哪分开模型,而且包围盒可以自由创建(只要包围盒平行于坐标轴并且包含分割面其中一侧的所有顶点)。
现在我们得到了所有的包围盒,下一步我们来构造一棵树。我们从最初的包围盒开始从上至下地反复分割它。另外,我们还可以用从下至上的方式,逐步地合并小包围盒从而得到最大的包围盒。把大的包围盒分割成小的包围盒,我们应该遵守以下几条原则。我们应该用一个面(这个面垂直于包围盒中的一条坐标轴)来分割包围盒上最长的轴,然后根据多边形处在分割轴的哪一边把多边形分离开来(如图7)。如果不能沿着最长的轴进行分割,那我们就沿第二长的边分割。我们持续地分割直到包围盒不能再分割为止。依据我们需要的精度(比如,是否我们真的要判断单个三角形的碰撞),我们可以按我们的选择的方式(如是按树的深度或是按包围盒中多边形的数目)以任意的条件停止分割。
正如你所看到的,创建阶段相当复杂,其中包括了大量的运算。很明显不能实时地创建树――只能是事先创建。事先创建可以免去实时改变多边形的可能。另一个缺点是OBB要求进行大量的矩阵运算,我们不得不把它们定位在适当的地方,并且每棵子树必须与矩阵相乘。
使用树进行碰撞检测
现在假设我们已经有了OBB或者AABB树。那么我们该怎么进行碰撞检测呢?我们先检测最大的包围盒是否相交,如果相交了,他们可能发生了碰撞,接下来我们将进一步地递归处理它们(不断地递归用下一级进行处理)。如果我们沿着下一级,发现子树并没有发生相交,这时我们就可以停止并得出结论没有发生碰撞。如果我们发现子树也相交了,那么要进一步处理它的子树直到到达叶子节点,并最终得出结论。进行相交测试时,我们可以把包围盒投影到空间坐标轴上并检查它们是否线性相交。这种给定的坐标轴称为分离坐标轴(separating axis)如图8所示。
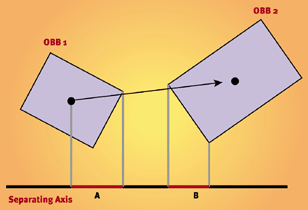
Figure 8. Separating axis (intervals
A and B don’t overlap).
为了快速地判断相交性,我们使用一种叫分离坐标的方法。这种方法告诉我们,只有15条潜在的分离坐标。如果跌交的情况在每一条分离坐标上都发生了,那么包围盒是相交的。因此,很容易就能判断出两个包围盒是否相交。
有趣的是,前面提到的时间片大小的问题用分离坐标技术很容易就能解决。回忆一下关于在两个给定时间内是否发生碰撞的问题。如果我们把速度加上,并且在所有15条坐标轴上的投影都跌交,说明会发生碰撞。我们可以用类似于AABB树那样的数据结构区分碰撞物和受碰物,并判断他们是否有可能发生碰撞。这种运算可以快速地排除在场景中的大多数情况,产生一个接近理想的O次幂(N logN)的效率。
基于BSP树的碰撞检测技术
BSP(二叉空间分割)树是另一种类型的空间分割技术,其已经在游戏工业上应用了许多年(Doom是第一个使用BSP树的商业游戏)。尽管在今天BSP树已经没像过去那么受欢迎了,但现在三个被认可的游戏引擎――Quake II, Unreal, and Lithtech(译者:这是2000年的文章,所以指出的这些游戏才这么老:)仍在广泛地采用这项技术。当你看一下BSP在碰撞检测方面那极度干净漂亮和高速的效率,立刻能让你眼前一亮。不但BSP树在多边形剪切方面表现出色,而且还能让我们有效地自由运用world-object式的碰撞检测。BSP树的遍历是使用BSP的一个基本技术。碰撞检测本质上减少了树的遍历或搜索。这种方法很有用因为它能在早期排除大量的多边形,所以在最后我们仅仅是对少数面进行碰撞检测。正如我前面所说的,用找出两个物体间的分隔面的方法适合于判断两个物体是否相交。如果分隔面存在,就没有发生碰撞。因此我们递归地遍历world树并判断分割面是否和包围球或包围盒相交。我们还可以通过检测每一个物体的多边形来提高精确度。进行这种检测最简单的一个方法是测试看看物体的所有部分是否都在分割面的一侧。这种运算真的很简单,我们用迪卡尔平面等式 ax + by + cz + d = 0 去判断点位于平面的哪一侧。如果满足等式,点在平面上;如果ax + by + cz + d > 0那么点在平面的正面;如果ax + by + cz + d < 0点在平面的背面。
在碰撞没发生的时候有一个重要的事情需要注意,就是一个物体(或它的包围盒)必须在分割面的正面或背面。如果在平面的正面和背面都有顶点,说明物体与这个平面相交了。
不幸的是,我们还没有一个很好的方法检测在一个时间间隔内的碰撞(在文章开头提到的方法现在仍在使用)。然而,我已经看到有另外的数据结构像BSP树一样开始广泛使用了。
曲面物体及碰撞检测
现在我们已经看到了两种多边形物体的碰撞检测,下面一看看如何计算弯曲物体的碰撞。99年发布的几款游戏已经大量地采用曲面了,因此在接下来几年里高效的曲面碰撞检测将变得十分重要。曲面碰撞检测(要求有给定点上精确的曲面等式)运算开销极大,所以我们要尽量避开它。实际上我们已经讨论了几种能用在这种情况下的方法。最明显的方法就是用低网格来近似表示曲面,然后使用这个多面体进行碰撞检测。甚至还有更简单的(但精度比较低),就是在曲面的控制顶点(译者:大概意思就是说每隔一定量的顶点就构造一个凸壳)上构造凸壳用来做碰撞检测。在这种情况下,曲面的碰撞检测十分近拟于传统的多面体碰撞检测。如图9显示了曲面及它在控制顶点上形成的凸壳。
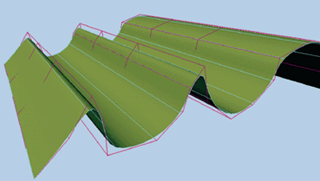
Figure 9. Hull of a curved object.
是否我们可以结合这两种技术形成一种混合方法?首先我们用凸壳进行碰撞检测然后逐步在凸壳所属的部分细分下去,这样就增加了精度。
由你决定
现在我们已经浏览了一些高级的碰撞检测(有一些也是基本的),你应该能够决定什么样的系统更适合你的游戏。你要决定的主要事情是精度、速度、实现的简单程度及系统的适应性。
For Further Info
H. Samet. Spatial Data Structures: Quadtree, Octrees and Other Hierarchical Methods. Addison Wesley, 1989.
For more information about AABBs take a look at J. Arvo and D. Kirk. “A survey of ray tracing acceleration techniques,” An Introduction to Ray Tracing. Academic Press, 1989.
For a transformation speedup, check out James Arvo’s paper in Andrew S. Glassner, ed. Graphics Gems. Academic Press, 1990.
S. Gottschalk, M. Lin, and D. Manocha. “OBBTree: A hierarchical Structure for rapid interference detection,” Proc. Siggraph 96. ACM Press, 1996. has contributed a great deal to the discussion of OBBs in terms of accuracy and speed of execution.
S. Gottschalk. Separating Axis Theorem, TR96-024, UNC Chapel Hill, 1990.
N. Greene. “Detecting intersection of a rectangular solid and a convex polyhedron,” Graphics Gems IV. Academic Press, 1994. introduces several techniques that speed up the overlap computation of a box and a convex polyhedron.
原文地址http://www.gamasutra.com/features/20000330/bobic_01.htm