http://www.cnblogs.com/flytrace/p/3379816.html
对于顶点来说,从object Space转换到eye space, 使用model-view矩阵就好了.那么顶点的法线是否也可以直接使用model-view矩阵转化?
通常情况下是不行的.
如下两张图是顶点的tangent和normal向量使用m-v矩阵从object space到eye space的变换:
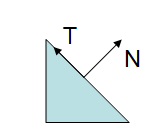
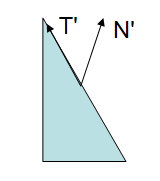
可以看到在eye-space中,tangent的方向仍符合定义,normal则不再垂直于tangent了.m-v矩阵不适用于normal.
令T为tangent,MV为model-view矩阵.P1, P2为tangent联系的2个顶点.
T = P2 - P1
T' = T * MV = (P2 - P1) * MV = P2 * MV - P1 * MV = P2' - P1'
因此T'保留了tangent的定义.但对于normal,你也可以找到N=Q2-Q1代表它,但是变换后Q2'-Q1'却不能保证垂直于T'.object space到view space,角度关系被改变了.
如何求出normal的变换,维持与tangent垂直?假设该变换为G.
normal与tangent垂直:
N'.T' = (GN).(MT) = 0
点积转化为叉积:
(GN).(MT) = (GN)T * (MT) = (GN)T(MT) = (NTGT)(MT) = NTGTMT = 0
注意到NTT为0:
若GTM = I,则上式成立.因此G=(M-1)T.
即normal matrix是model-view矩阵的逆矩阵的转置矩阵.
若model-view矩阵是一个正交矩阵,则G=M.这便是例外情况下normal matrix为model-view矩阵.
Part1 转换流程之顶点转换
物体顶点是相对于物体自身坐标系而言的数据,要进行一系列转换才最后显示在屏幕上:
1.物体坐标系到世界坐标系。
乘以World矩阵,包含了物体的平移旋转和缩放。
2.世界坐标系到相机坐标系。
乘以View矩阵。
该矩阵实际上是相机相对于世界坐标系转换的逆矩阵。
所以相机的世界坐标系位置可以用View矩阵的逆矩阵的平移向量表示出来。
3.相机坐标系到标准视体空间的变换。
乘以Projection矩阵。
根据Projection矩阵的不同,有正交和投影变换两种结果。
这步操作的实际意义是将视锥空间内的点变换进入一个标准观察体,从而方便剪裁。
不同API标准观察体的设置不同:
DirectX的标准观察体最小拐角(-1,-1,0)最大拐角(1,1,1),
OpenGL最小拐角(-1,-1,-1)最大拐角(1,1,1),二者区别在于Z的范围不同。
注意透视变换是非线性变换,会使得w值变化,不再是1。
4.完成剪裁后接着对应到屏幕空间。
这步完成3D到2D的映射,对应成屏幕像素显示。
说明:以上只是对顶点变换的简单介绍,还有很多没有详细讨论的地方。
因为关于3D流水线的很多地方感觉理解的不是很实在,所以以后有空的时候再总结吧。
Part2 转换流程之法向量变换
光照计算常常需要用法向量,但是法向量的转换和顶点转换并不完全相同。
不同点主要体现在上述过程中的第一步。即从物体坐标系变换到世界坐标系。
首先法向量表示的是方向,平移是不必要的。(由于法向量多是3D向量或第四位为0,其实变换矩阵的平移部分是不起作用的)。
那么法向量变换就只剩旋转和缩放。
而法向量的旋转和顶点的旋转保持一致即可,因为转过的角度是相同的。
但是直接用World矩阵直接对法向量进行变换有可能是不对的!!
为什么呢,主要就是在于缩放有可能不是三个坐标方向的等比例缩放。
因为如果模型被不成比例的缩放,在不同方向上会有不同程度的拉伸或者压缩,顶点的坐标会因而伸缩。
但是如果对法向量进行同样的伸缩,那么法向量将不再垂直于对应的表面(顶点的法向量是该顶点所在几个表面法向量的平均值)。
此时要对法向量进行正确的变换,应该是对其进行相反的缩放(比如xy是1:2缩放,那么法向量xy就要2:1缩放。)
所以法向量的变换矩阵中缩放矩阵应该是原来顶点变换缩放矩阵的逆矩阵。
这个怎么做到呢,如前所述,缩放矩阵并不是正交矩阵,不能通过转置来得到逆矩阵。直接对原来的world矩阵求逆的话,旋转的部分也同时被求逆了。但是旋转又要求用原来的旋转。
但是旋转矩阵是正交矩阵,转置后即可得到逆矩阵。
于是可以采用这样的方法:对World矩阵求逆,这样就同时得到了旋转和缩放的逆,然后进行转置再将旋转矩阵变回来,因为缩放系数在对角线上所以不会有影响。这样得到的变换矩阵就可以用来正确变换法向量了。
关于转置,可以变换矩阵和向量相乘的顺序,这样就相当于和转置矩阵相乘了。
所以要做的只是求出逆矩阵,然后变换矩阵和向量原来的相乘顺序。
注意就是因为法向量变换的问题是由于非等比例缩放引起的,如果原来的World矩阵三个方向缩放系数相等,那么用原来的World矩阵变换法向量是没有问题的。