最简单的斜率优化的双语详解

最简单的斜率优化的双语详解

English-speaker can click here 

本蒟蒻自己也没有很搞懂斜率优化，只是简单记录一下，方便自己将来复习。

一道题的引入 

用一道很经典的题目来引入斜率优化。

原题 

HDU3507

Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly. 

 (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000)

题意

给你一个序列a₁~a_n，你可以在任意的位置花费M来换一次行（第一行也算一次换行）。你的总花费为之前所有的花费和每一行的和的平方。

P.S:  这个n小于等于500000

解析 

先考虑一下，如果不管n的取值，范围会怎么做。

首先，我们考虑一下，这道题的题意，我们很容易发现，如果我选择在第i个位置换行，对于a_i之前的所有选择没有影响，所有很容易就想到了dp。

我们用f[i] 来表示当我已经做到了第i个的时候，我的最小花费。

然后呢，我们要尝试来维护这个式子。

首先最无脑的方法，也是最普遍的方法，假设第i个之前的换行为j，然后在将j从1跑到i，寻找最小的f[j]+(sum[i] - sum[j-1])²+M，然后转移状态。

这里的sum[i]是预处理好前i个数的的前缀和。

显然这样的做法不是正解，这种算法的复杂度是O（n²），显然这会超出时间限制，那么这样，我们的主角就出现了。

斜率优化

主角出现了

先推推式子

我们很容易可以根据上面的式子推出以下这些奇怪的东西:

设当前正在转移状态的是i，k < j < i.
然后， 我们可以根据上面的式子得到，如果(sum[i]-sum[k-1])² + f[k] + M < (sum[i]-sum[j-1])² + f[j] + M 那么我们一定会选择转移k的状态而不是j的

那么我们化简这个式子，可以得到：

sum[k-1]² - 2*sum[k-1]*sum[i] + f[k] < sum[j-1]² - 2*sum[j-1]*sum[i] + f[j].

合并同类项

2*sum[i]*(sum[j-1]-sum[k-1]) < f[j]-f[k]+sum[j-1]²-sum[k-1]²

然后两边同除以(sum[j-1]-sum[k-1])

得到

2*sum[i] < (f[j]-f[k]+sum[j-1]²-sum[k-1]²) / (sum[j-1]-sum[k-1])

斜率的使用

很容易的知道不等式左侧在同一步操作中是一个常数，并且是一直可知的，所以我们只考虑右侧的多项式。

仔细观察，如果我们定义一个新的函数g(x) = f[x]+sum[x-1]²，我们是不是可以得到一个很谐有趣的事情

g(j) - g(k) / sum[j-1]-sum[k-1]

像不像一条线的斜率？

然后我们可以搭建一个直角坐标系，横坐标为sum[i]，纵坐标为g(i)

根据这个满足不等式的话，我们会优先选择较大的点，否则则选择较小的。

所以我们选择的点应该是斜率小于2*sum[i]的最大斜率的边的终点，大于2*sum[i]的最小边的起点。

优化

很显然，这么一波猛如虎的操作，并没有从根本上降低O(n²)的复杂度，所以接下来我们就要来走完从O(n²)到O(n)的距离。

然后，在这里，我们考虑如果要满足上述，要求，那么我们所选的点应该一定满足斜率的单调递增。于是，我们可以使用凸包。

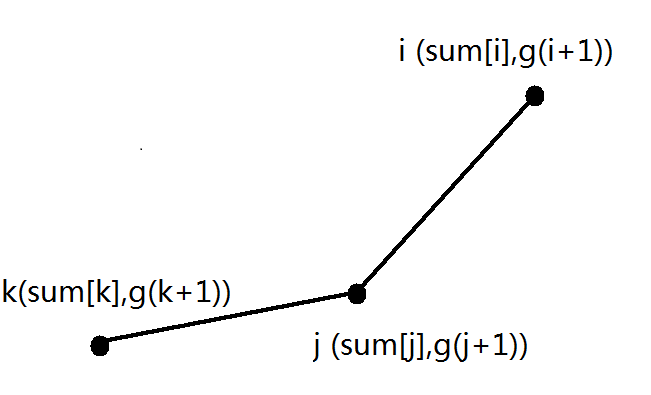
没错，就是这个样子的图形，但为什么只要考虑凸包就可以不遗漏的考虑完所有的可能?

考虑一下有一个点d在k,j,i之间那么jd的斜率一定小于ji且大于kj，显然更加难以符合上述的条件，所以我们只需要考虑凸包即可。

但是这里还有一个问题，那就是，其实凸包这一个优化也没有降低该算法的多项式复杂度，但是，我们考虑到凸包有一个性质，那就是斜率单调递增，而2*sum[i]也是单调递增，所以我们可以使用单调队列维护，所以这样的复杂度就会被降到了

O(n)，考虑单调队列的复杂度，所以这个算法是均摊O（n）的。

最后，贴代码。

#include<bits/stdc++.h>
using namespace std;
int a[500101];
int sum[500101];
int que[500101];
int dp[500101];
bool cal(int ax,int ay,int bx,int by,int cx,int cy)
{
    return (ax-bx)*(cy-by)>=(ay-by)*(cx-bx);
}
int gety(int x)
{
    return dp[x-1]+sum[x-1]*sum[x-1];
}
int getx(int x)
{
    return sum[x-1];
}
int get(int i,int ss)
{
    return gety(i)-2*ss*getx(i);
}
int main()
{
    int n,m;
 
    while(scanf("%d%d",&n,&m) != EOF)
    {
    memset(sum,0,sizeof(sum));
    memset(dp,0,sizeof(dp));
    for(int i = 1;i <= n;i++)
    {
        scanf("%d",&a[i]);
        sum[i] = sum[i-1] +  a[i];
    }
    int head = 0,tail = -1;
    for (int i = 1;i <= n;i++)
    {
        while(head < tail && cal(getx(que[tail-1]),gety(que[tail-1]),getx(que[tail]),gety(que[tail]),getx(i),gety(i)))
        {
            tail--;
        }
        que[++tail] = i;
        while(head < tail && get(que[head],sum[i]) >= get(que[head+1],sum[i]))
        {
            head++;
        }  
        dp[i] = get(que[head],sum[i]) + m + sum[i]*sum[i];
    }
    printf("%d
",dp[n]);
    }
    return 0;  
}