超几何分布
产品抽样检查中经常遇到一类实际问题,假定在N件产品中有M件不合格品,即不合格率
 。
。
在产品中随机抽n件做检查,发现k件不合格品的概率为
 ,k=0,1,2,...,min{n,M}。
,k=0,1,2,...,min{n,M}。
Numpy中的超几何分布
Numpy的random包中提供了产生超几何分布结果的函数:
numpy.random.hyermetric(ngoog,nbad,nsample,size=None)
https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.hypergeometric.html
- ngood: 做出好的选择的数量,相当于上面的N件产品中的合格品,即N-M;
- nbad:做出坏的选择的数量,相当于上面的M件合格品;
- nsample:每次的采样数;
- size:采样的组数,即试验组数.
上面的hypermetric()函数返回一组size大小的数组,数组中的每个数是在一组采样中合格产品的数量,即上面的k.
下面我们用一个具体的做游戏的例子来说明这个函数的用法:
一个袋子中有20个球,其中有1个黑球,别的都是红球.从袋子中每次取3个球,如果3个都是红球加1分,如果其中有一个黑球就减4分.我们用程序来模拟100次试验以后的得分情况,并绘制出得分的变化图.
(为了方便,以下代码是在ipython -pylab运行的)
1 使用hypermetric()初始化100组试验的结果,并初始化一个分数数组.
# 初始化一个计分板 points = zeros(100) # 使用超几何分布初始化每次实验结果 # outcomes数组中的每一个项都是一次试验中取得红球的个数 # 注意第一个参数是红球个数,即为19而不是20 outcomes = random.hypermetric(19,1,3,size = len(points))
2 根据每一次模拟试验的结果来设置分数
for i in range(len(points)): if outcomes[i] == 3: points[i] = points[i-1] + 1 elif outcomes[i] == 2: points[i] = points[i-1] - 4 else: print(outcomes[i])
3 利用matplotlib绘制分数变化的曲线
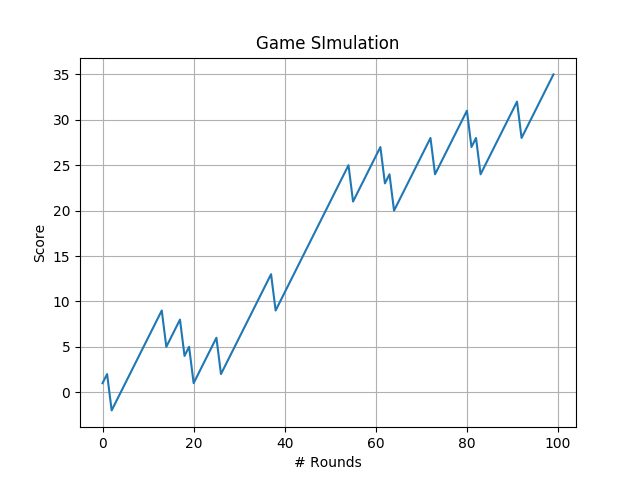
plt.plot(np.arange(len(points)),points) plt.title("Game SImulation") plt.xlabel('# Rounds')
plt.ylabel('Score')
plt.grid()
plt.show()
4 分数变化的曲线如下