背包问题扩展【动态规划】

【题目】先给出题目的链接

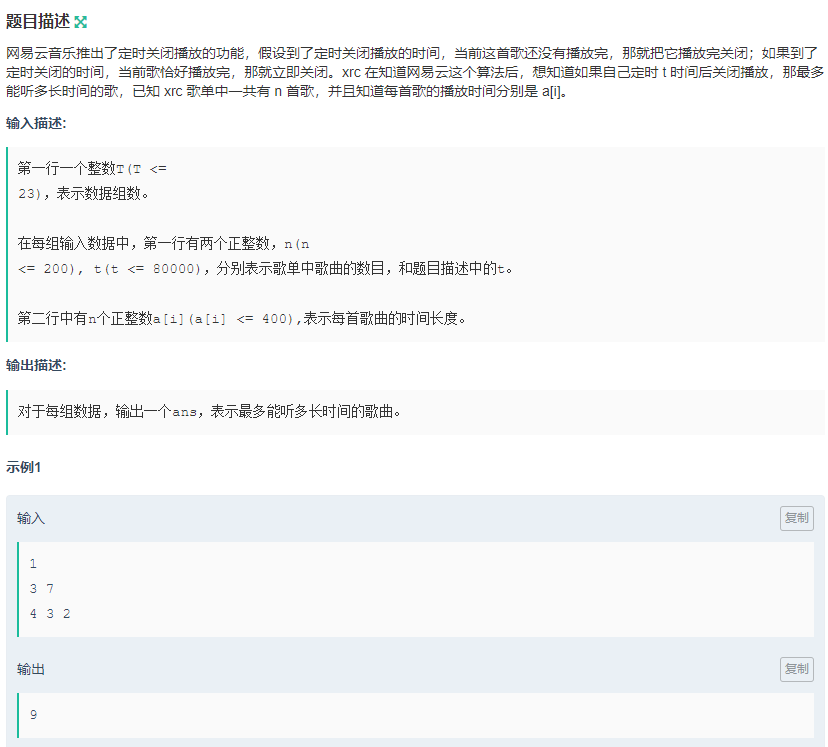
【分析】
题目有点类似于宝背包问题，算是一种背包问题的变形。首先我们要留出背包容量为1来装价值最大的东西，剩下的背包体积还有其他物品就按照01背包的解题思路去求解。最后问题的答案就是：价值最大的东西的价值+剩余空间dp[]之后的最大价值。
如果把背包容量完全给了去dp[]求解的话，求得的最终价值并不是最大的，这个问题仔细思考一下就不难发现。因为当体积刚好用完的时候，就不能在去装东西了。但是留有1的体积给最大的价值物品之后，我们保证了最大价值的物品一定能够被选上，
其他剩余的体积去DP就不会出错。
【代码】

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef unsigned long long int ull;
const int maxn=100005;
int main()
{
    ll t,n,k;
    scanf("%lld",&t);
    while(t--)
    {
        scanf("%lld %lld",&n,&k);
        ll w[maxn] = {0},dp[maxn] = {0};
        for(int i=1;i<=n;i++)
            scanf("%lld",&w[i]);
        sort(w+1,w+n+1);
        for(int i=1;i<=n-1;i++)
        {
            for(int j=k-1;j>=w[i];j--)
            {
                dp[j] = max(dp[j],dp[j-w[i]] +w[i]);
            }
        }
        printf("%lld
",dp[k-1]+w[n]);
    }
    return 0;
}

【补充】
一维数组的dp可以节约空间复杂度，比二维数组更为高效易懂。