题意:

T <= 10000
N, M<=10000000
思路:同BZOJ2154


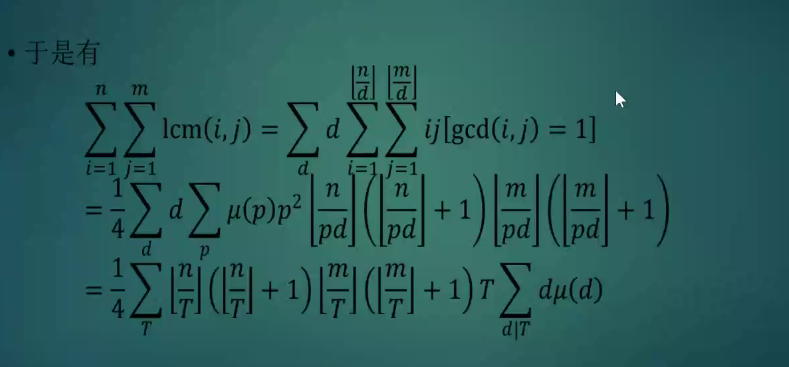
From http://www.cnblogs.com/ST-Saint/p/4617247.html
对于一个素数p,它的新 h 值显然是 p - p^2 的
如果 p 是多个素数的一次项的积
显然 h 是积性的 h( p ) = h( p1 ) * h( p2 ) * h( p3 )……
如果 p 的唯一分解可以写成一部分素数乘积 i 与 另一部分在前一部分中出现过的素数的乘积 j,也就是存在质因子的指数大于1,它新增的每一个因子的 μ 值都是0,没有意义,只有统计时D变成了原来的 j 倍
所以 此时 h( p ) = h( i ) * j
1 const mo=100000009; 2 max=10000000; 3 var flag,prime:array[0..max]of longint; 4 sum,f:array[0..max]of int64; 5 cas,v,n,m,i,j,t:longint; 6 7 function min(x,y:longint):longint; 8 begin 9 if x<y then exit(x); 10 exit(y); 11 end; 12 13 function clac(x,y:int64):int64; 14 begin 15 x:=x*(x+1) div 2 mod mo; 16 y:=y*(y+1) div 2 mod mo; 17 exit(x*y mod mo); 18 end; 19 20 function query(n,m:longint):int64; 21 var i,x,y,pos,t:longint; 22 begin 23 i:=1; query:=0; 24 if n>m then begin t:=n; n:=m; m:=t; end; 25 while i<=n do 26 begin 27 x:=n div i; y:=m div i; 28 pos:=min(n div x,m div y); 29 query:=query+clac(x,y)*(sum[pos]-sum[i-1]) mod mo; 30 query:=(query mod mo+mo) mod mo; 31 i:=pos+1; 32 end; 33 end; 34 35 begin 36 assign(input,'bzoj2693.in'); reset(input); 37 assign(output,'bzoj2693.out'); rewrite(output); 38 f[1]:=1; 39 for i:=2 to max do 40 begin 41 if flag[i]=0 then 42 begin 43 inc(m); prime[m]:=i; 44 f[i]:=(i-int64(i)*i) mod mo; 45 end; 46 j:=1; 47 while (j<=m)and(prime[j]*i<=max) do 48 begin 49 t:=prime[j]*i; flag[t]:=1; 50 if i mod prime[j]=0 then 51 begin 52 f[t]:=prime[j]*f[i] mod mo; 53 break; 54 end; 55 f[t]:=f[prime[j]]*f[i] mod mo; 56 inc(j); 57 end; 58 end; 59 for i:=1 to max do sum[i]:=(sum[i-1]+f[i]) mod mo; 60 read(cas); 61 for v:=1 to cas do 62 begin 63 read(n,m); 64 writeln(query(n,m)); 65 end; 66 close(input); 67 close(output); 68 end.