谱聚类(上篇)

谱 图 理 论

-->引言

谱图理论是图理论与线性理论的组合。首先，用矩阵来表示图；其次，求该矩阵的特征值和特征向量；最后，通过特征值和特征向量来分析图的性质。其中，谱指该矩阵所有特征值的集合，图指图论中的图。

-->图的基本定义

在数学中，图是由顶点(Vertex、node)以及连接顶点的边(edge)构成。顶点表示研究对象，边表示两个对象之间特定的关系。
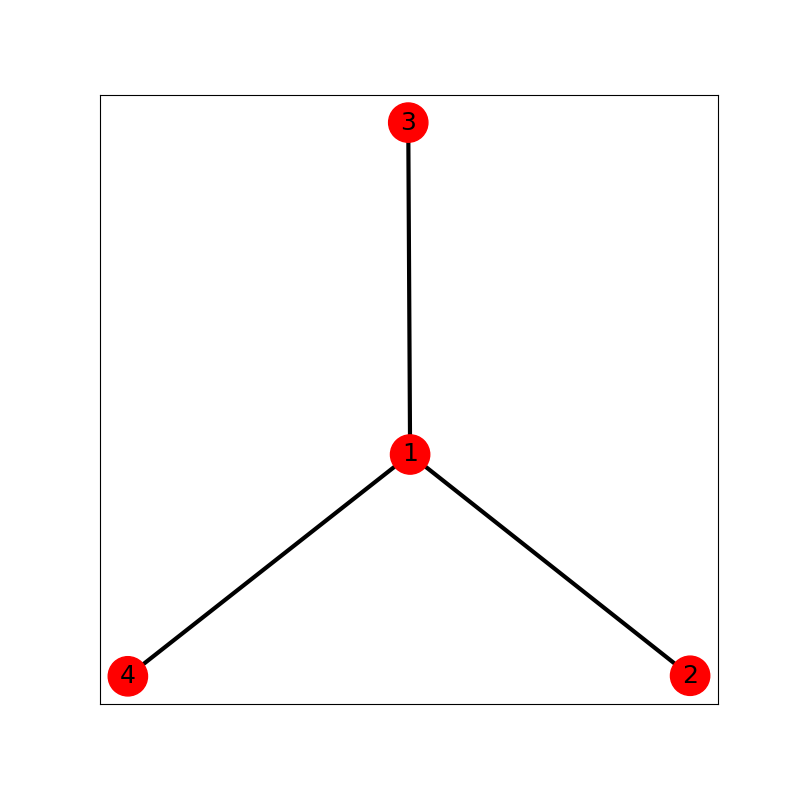
图表示顶点和边的集合，记(G=(V,E))。其中(V)表示顶点集合，(E)表示边集合。如下图所示：

import networkx as nx
import matplotlib.pyplot as plt

# 添加顶点
plt.figure(figsize=(10, 10))
G = nx.Graph()
G.add_node(1)
G.add_node(2)
G.add_node(3)
G.add_node(4)
# 添加边
G.add_edge(1, 2, weight=5)
G.add_edge(1, 4, weight=5)
G.add_edge(1, 3, weight=10)

# 添加顶点列表及对应的颜列表并可视化
nx.draw_networkx(G, nodelist=[1, 2, 3, 4], font_size=18, width=3, node_size=[800, 800, 800, 800],
                 node_color=["r", "r", "r", "r"])
plt.show()

-->图的基本类型

(1) 有向图和无向图
如果图中的边存在方向性，则称这样的边为有向边(e_{ij}=<v_i, v_j>)，其中(v_i)是这条边的起点，(v_j)是有向边的终点，包含有向边的图为有向图。与有向图相对应的图称为无向图。在无向图中，边是没有方向的，即(e_{ij}=<v_i, v_j>=<v_j, v_i>=e_{ji})。

(2) 非加权图与加权图
如果图里的每条边与实数对应，我们称这样的图为加权图。该实数称为对应边的权重。反之，为非加权图。

(3) 连通图与非连通图
如果图中存在孤立的顶点，没有任何边与之相连，这样的图称为非连通图。反之，称为连通图。

(4) 邻居
如果存在一条边连接两个顶点(v_i)和(v_j)，则称这两个顶点互称为邻居。

(5) 度
以(v_i)为端点的边的数目称为(v_i)的度(Degree)。

(6) 度与边的关系
在图中，所有节点的度之和是所有边的两倍，公式如下:

[sum_{v_i}deg(v_i)=2|E| ]

在有向图中，顶点的度数等于顶点的出度与入度之和。

(7) 子图
如果图(G^{'}=(V^{'}, E^{'}))的顶点集和边集分别是另一个图(G=(V, E))的顶点集和边集的子集，即(V^{'}subseteq{V},E^{'}subseteq{E}),则称图(G^{'})是图(G)的子图。

-->图的储存和遍历

(1) 邻接矩阵和关联矩阵
邻接矩阵(A)描述中顶点之间的关联，(Ain{R^{N imes{N}}}),其定义为：

[ A_{ij}= egin{cases} 1, & ext {if $(v_i, v_j)subseteq{E}$} \ 0, & ext {else} end{cases} ]

用邻接矩阵储存图的时候，需要一个一维数组表示顶点集合，需要一个二维数组表示邻接矩阵。实际开发中，邻接矩阵往往会出现大量0值，因此可以用稀疏矩阵格式来储存邻接矩阵。
有时候，我们用关联矩阵(Bin{R^{N imes{N}}})来描述节点与边的关系，定义如下：

[ B_{ij}= egin{cases} 1, & ext {if $v_i$与$e_j$相连} \ 0, & ext {else} end{cases} ]

用关联矩阵储存图的时候，需要两个一维数组分别表示顶点集合和边集合，需要一个二维数组表示关联矩阵。
(2) 图的遍历
图的遍历是指从图中的某个顶点出发，按照某种搜索算法沿着图中的边对图中的所有顶点访问一次。
图的遍历主要有两种算法：
【深度优先搜索】
深度优先搜索时一个递归算法，有回退的过程。算法思想：从图中某个顶点(v_i)开始，由(v_i)出发，访问它的任意一个邻居(w_1)，访问(w_1)的所有邻居中未被访问过的顶点(w_2)；然后，从(w_2)出发，依次访问，直到出现某个顶点不再有邻居未被访问。接着，回退一步到前一次刚被访问过的顶点，看是否还有未被访问过的邻居，如果有，则访问该邻居，之后再从该邻居出发，进行与前面类似的访问；如果没有，就再退一步进行类似的访问。重复上述过程，直到该图所有顶点都被访问过为止。

【广度优先搜索】
广度优先搜索时一个分层的搜索过程，没有退回过程。算法思想：从图中的某个顶点(v_i)开始，由(v_i)出发，依次访问(v_i)的所有未被访问过的邻居(w_1,w_2,...,w_n),然后再顺序访问(w_1,w_2,...,w_n)的所有未被访问的邻居，一层层的执行下去，直到所有顶点被访问到为止。

-->拉普拉斯算子

(1) 微分中的拉普拉斯算子
拉普拉斯算子是(n)维欧几里得空间中的一个二阶微分算子，定义为梯度的散度(散度衡量一点处的向量场是发散还是吸收)，如果(f)是二阶可微函数，则(f)的拉普拉斯算子：

[Delta{f}= abla^{2}f ]

(f)的拉普拉斯算子也是笛卡尔坐标系中的所有非混合二阶偏导数：

[Delta{f}=sum_{i=1}^{n}frac{partial^2{f}}{partial^2{x_i^2}} ]

(2) 导数的定义
【一元函数】
设函数(y=f(x))在点(x_0)的某个领域内有定义，当自变量(x)在(x_0)处有增量(Delta{x}),相应地函数取得增量(Delta{y}=)( Delta{f}=f(x_0+Delta{x})-f(x_0)),则在(x_0)点处(f(x))的导数的近似计算公式如下：

[f^{'}(x)approxfrac{f(x+Delta{x})-f(x)}{Delta{x}} ]

对于二阶导数，近似计算公式如下：

[f^{'}(x)approxfrac{f^{'}(x)-f^{'}(x-Delta{x})}{Delta{x}} approx frac{frac{f(x+Delta{x})-f(x)}{Delta{x}}-frac{f(x)-f(x-Delta{x}))}{Delta{x}}}{Delta{x}}\ =frac{f(x+Delta{x})+f(x-Delta{x})-2f(x)}{Delta{x}^2} ]

【二元函数】
拉普拉斯算子可以用下面近似公式计算：

[Delta{f}=frac{partial^2{f}}{{partial{x}^2}}+frac{partial^2{f}}{{partial{y}^2}}\ approxfrac{f(x+Delta{x},y)+f(x-Delta{x},y)-2f(x,y)}{Delta{x}^2}+frac{f(x,y+Delta{y})+f(x,y-Delta{y})-2f(x,y)}{Delta{y}^2} ]

对上面的二元函数进行离散化，对自变量的一系列点处的函数值进行采样，得到下面一系列点处的函数值，构成一个矩阵

[left[egin{matrix} f(x_1,y_1) & f(x_2,y_1) & ... & f(x_n,y_1)\ f(x_1,y_2) & f(x_2,y_2) & ... & f(x_n,y_2)\ ... & ... & ... & ...\ f(x_1,y_n) & f(x_2,y_n) & ... & f(x_n,y_n) end{matrix} ight] ]

点((x_i,y_i))处的拉普拉斯算子计算公式(这里(Delta=1),即(Delta{x}=x_{i+1}-x_{i}=1),(Delta{y}=y_{i+1}-y_{i}=1))：

[frac{f(x_i+Delta{x},y_j)+f(x_i-Delta{x},y_j)-2f(x_i,y_j)}{Delta{x}^2}+frac{f(x_i,y_j+Delta{y})+f(x_i,y_j-Delta{y})-2f(x_i,y_j)}{Delta{y}^2}\ =frac{f(x_{i+1},y_j)+f(x_{i-1},y_j)-2f(x_i,y_j)}{1^2}+frac{f(x_i,y_{j+1})+f(x_i,y_{j-1})-2f(x_i,y_j)}{1^2}\ =f(x_{i+1},y_j)+f(x_{i-1},y_j)+f(x_i,y_{j+1})+f(x_i,y_{j-1})-4f(x_i,y_j) ]

-->图的拉普拉斯矩阵

从上面的公式可以看出，一个点的拉普拉斯算子只与相邻的四个采样点有关。下面需要将拉普拉斯算子进行推广。如果将图的顶点处的值看作函数值，则该顶点(i)处的拉普拉斯算子为

[Delta{f_i}=sum_{jin{N_i}}(f_j-f_i) ]

其中(N_i)是顶点(i)的所有邻居顶点集合。当图的边带有权重的时候，计算公式如下：

[Delta{f_i}=sum_{jin{N_i}}w_{ij}(f_j-f_i) ]

如果(j otin{N_i}),则(w_{ij}=0)。所以上式可以写成：

[Delta{f_i}=sum_{jin{V}}w_{ij}(f_j-f_i)=sum_{jin{V}}w_{ij}f_j-sum_{jin{V}}w_{ij}f_i=w_if - d_if_i ]

其中，(w_i)是邻接矩阵的第(i)行，(d_i)是顶点(i)的加权度。
对于图的所有顶点，我们有

[left[egin{matrix} Delta{f_1}\ Delta{f_2}\ ...\ Delta{f_n} end{matrix} ight] = left[egin{matrix} w_1f - d_1f_1\ w_2f - d_2f_2\ ...\ w_nf - d_nf_n end{matrix} ight] = left[egin{matrix} w_1\ w_2\ ...\ w_n end{matrix} ight] left[egin{matrix} f_1\ f_2\ ...\ f_n end{matrix} ight] - left[egin{matrix} d_1 & ... & 0\ 0 & d_2 & 0\ ... & ... & ...\ 0 & ... & d_n end{matrix} ight] left[egin{matrix} f_1\ f_2\ ...\ f_n end{matrix} ight]\ =(W-D)f ]

上述就是拉普拉斯矩阵的推导过程。其中W为邻接矩阵，D为加权度矩阵。