题意:
给出一个n*m的地图,要求从左上角(0, 0)走到右下角(n-1, m-1)。
地图中每个格子中有一个值。然后根据这些值求出一个最小值。
这个最小值要这么求——
这是我们从起点走到终点的路径,其中N是地图的长,M是地图的宽,Ai表示路径中第i个点的值,Aavg表示路径中所有的点的值的平均值。要求这个式子的值最小。
我们可以将它转化为
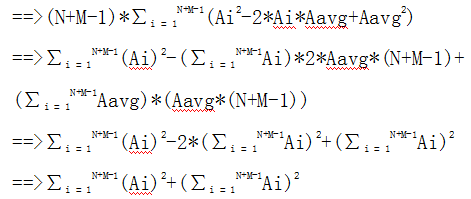
好了,推到这里,我们需要的数学知识就结束了(实际上以我的数学知识也只能做到这里了……)。然后dp就好了——
Dp[i][j][k],i表示第i行,j表示第j列,k表示所有Ai的和,这个里面保存的是所有  的值。
的值。
然后dp下去就好了.
dp[i][j][k] = min(dp[i][j][k], dp[i-1][j][k-mp[i-1][j]]+mp[i][j]*mp[i][j], dp[i][j][k-mp[i][j-1]]+mp[i][j]*mp[i][j]);
具体见代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 #include <algorithm> 5 using namespace std; 6 const int M = 1000010; 7 const int Mod = 100000; 8 const int N = 33; 9 const int NN = 1800; 10 11 int t, n, m; 12 int dp[N][N][NN], mp[N][N]; 13 int ans; 14 15 int Min(int x, int y) 16 { 17 if(x == -1) return y; 18 return x < y ? x : y; 19 } 20 21 void Dp() 22 { 23 memset(dp, -1, sizeof(dp)); 24 dp[0][0][mp[0][0]] = mp[0][0]*mp[0][0]; 25 for(int i = 0; i < n; i++) 26 { 27 for(int j = 0; j < m; j++) 28 { 29 if(i-1 >= 0) 30 { 31 for(int k = mp[i][j]; k < NN; k++) 32 { 33 if(dp[i-1][j][k-mp[i][j]] != -1) 34 { 35 dp[i][j][k] = Min(dp[i][j][k], dp[i-1][j][k-mp[i][j]]+mp[i][j]*mp[i][j]); 36 } 37 } 38 } 39 if(j-1 >= 0) 40 { 41 for(int k = mp[i][j]; k < NN; k++) 42 { 43 if(dp[i][j-1][k-mp[i][j]] != -1) 44 { 45 dp[i][j][k] = Min(dp[i][j][k], dp[i][j-1][k-mp[i][j]]+mp[i][j]*mp[i][j]); 46 } 47 } 48 } 49 } 50 } 51 } 52 53 int main() 54 { 55 //freopen("test.in", "r", stdin); 56 scanf("%d", &t); 57 for(int tm = 1; tm <= t; tm++) 58 { 59 scanf("%d%d", &n, &m); 60 for(int i = 0; i < n; i++) 61 { 62 for(int j = 0; j < m; j++) scanf("%d", &mp[i][j]); 63 } 64 Dp(); 65 ans = -1; 66 for(int i = 0; i < NN; i++) 67 { 68 if(dp[n-1][m-1][i] != -1) 69 { 70 int mid = (n+m-1)*dp[n-1][m-1][i]-i*i; 71 if(ans == -1) ans = mid; 72 else ans = ans < mid ? ans : mid; 73 } 74 } 75 printf("Case #%d: %d ", tm, ans); 76 } 77 return 0; 78 }
