布隆过滤器

首先看一下wiki上开篇对布隆过滤器的总体介绍：

A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set. False positive matches are possible, but false negatives are not – in other words, a query returns either "possibly in set" or "definitely not in set". Elements can be added to the set, but not removed (though this can be addressed with a "counting" filter); the more elements that are added to the set, the larger the probability of false positives.

中文大体意思如下：

　　布隆过滤器是一个空间效率比较高的数据结构，由Burton Howard Bloom在1970年构思出来，用于检测一个元素在集合中是否存在。对于“存在”的结论，有误判的可能；对于“不存在”的结论是正确无疑的，不存在误判的可能。可以向布隆过滤器添加元素，但是不能删除（带“计数”功能的可以）；布隆过滤器添加的元素越多，误判的概率越高。

布隆过滤器定义：

An empty Bloom filter is a bit array of m bits, all set to 0. There must also be k different hash functions defined, each of which maps or hashes some set element to one of the m array positions, generating a uniform random distribution. Typically, k is a constant, much smaller than m, which is proportional to the number of elements to be added; the precise choice of k and the constant of proportionality of m are determined by the intended false positive rate of the filter.

布隆过滤器是一个m位bit位数组，对于空的布隆器，所有bit位为0。还需定义k个不同的hash函数，对于一个元素均匀随机散列到bit数组上（注：散列到的bit位设置为1）。通常k是一个远比m小的常量，m与要添加的数据总量成正比；基于一个预定的误判率去选择设置k和

添加：

To add an element, feed it to each of the k hash functions to get k array positions. Set the bits at all these positions to 1.

查询：

To query for an element (test whether it is in the set), feed it to each of the k hash functions to get k array positions. If any of the bits at these positions is 0, the element is definitely not in the set – if it were, then all the bits would have been set to 1 when it was inserted. If all are 1, then either the element is in the set, or the bits have by chance been set to 1 during the insertion of other elements, resulting in a false positive.

由上可见，添加和查询都要对元素使用k个hash函数，

对于添加，作用是用于定位哪些bit位置需要标1；对于查询，作用是拿散列出来的位置去比对现有的bit数组上的标记，对应的位置只要有0存在，则说明元素一定不存在，如果都是1，则有可能存在，也有可能是误判。

 

范例：

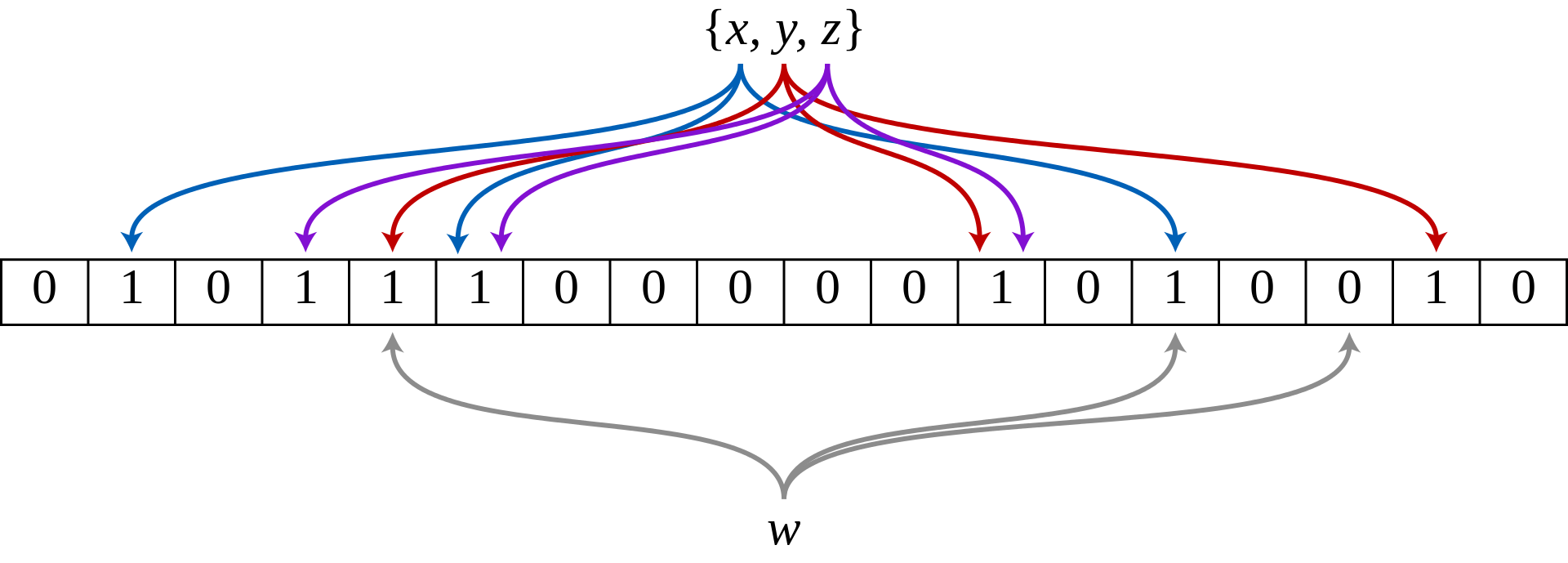
An example of a Bloom filter, representing the set {x, y, z}. The colored arrows show the positions in the bit array that each set element is mapped to. The element w is not in the set {x, y, z}, because it hashes to one bit-array position containing 0. For this figure, m = 18 and k = 3.

上图中，关于添加，对于元素x,y,z使用3个散列函数进行散列，被散列到的bit位会标1；查询w，由于最后一个散列到的bit位是0，断定w一定不存在集合中。

数学公式：

 这里的n是数据总量，p是容忍的误判率；

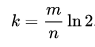
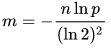
应用：

围绕两点：

　　1.不存在，就是一定不存在 ；

　　2.存在，可能是误判，只是误判的几率依照一般预设的误判率会很小，比如0.01% ； 

布隆过滤器被广泛用于网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统以及解决缓存穿透问题。

黑名单（黑名单数据全部放入布隆过滤器，访问的用户存在，则进行拦截），垃圾邮件地址（逻辑类似黑名单），缓存穿透（将所有可能的数据存放到布隆过滤器中，用户访问不存在的数据直接返回）

注 ：缓存穿透 指的是，查询的数据在数据库中压根不存在，缓存中当然也不存在 。另外， 缓存击穿 是指缓存中没有但数据库中有的数据（一般是缓存时间到期），这时由于并发用户特别多，同时读缓存没读到数据，又同时去数据库去取数据，引起数据库压力瞬间增大，造成过大压力；缓存雪崩 是指缓存中数据大批量到过期时间，而查询数据量巨大，引起数据库压力过大甚至down机。和缓存击穿不同的是，缓存击穿指并发查同一条数据，缓存雪崩是不同数据都过期了，很多数据都查不到从而查数据库。

快速使用，

 推荐使用guava中的com.google.common.hash.BloomFilter ；

 public void testBoolmFilter() {
        //总量
        int size = 1000_000;
        //误判率
        double fpp = 0.01;
        BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size, fpp);
        for (int i = 0; i < size; i++) {
            bloomFilter.put(i);
        }

        List<Integer> list = new ArrayList<Integer>(1000);
        // 故意取100000个不在过滤器里的值，看看有多少个会被认为在过滤器里
        for (int i = size + 100000; i < size + 200000; i++) {
            if (bloomFilter.mightContain(i)) {
                list.add(i);
            }
        }
        System.out.println("误判的数量：" + list.size() + " ,误判率为： " + list.size() / 100000.0);

        long start = System.nanoTime();
        int times = 100_000_000;
        for (int i = 0; i < times; i++) {
            if (bloomFilter.mightContain(i)) {
            }
        }

        long end = System.nanoTime();
        System.out.println("平均单次查询耗时 " + (end - start) / times + " ns");

        System.out.println("平均单次查询耗时 " + TimeUnit.NANOSECONDS.toMillis(end - start) / times + " ms");
    }

 输出如下：

误判的数量：1052 ,误判率为： 0.01052
平均单次查询耗时 118 ns
平均单次查询耗时 0 ms

参考：https://en.wikipedia.org/wiki/Bloom_filter ;

          https://blog.csdn.net/fouy_yun/article/details/81075432 ;