1.用二进制数表示小数
主要是小数部分乘以2,取整数部分依次从左往右放在小数点后,直至小数点后为0
2.什么是浮点数
浮点数是指用符号,尾数,基数和指数这四部分来表示的小数。因为计算机内部使用的是二进制数,所以基数自然是2。因此,实际的数据中往往不考虑基数,只用符号,尾数,指数这三部分即可表示浮点数。
也就是说,64位(双精度浮点数)和32位(单精度浮点数)的数据,会被分为三部分来使用。
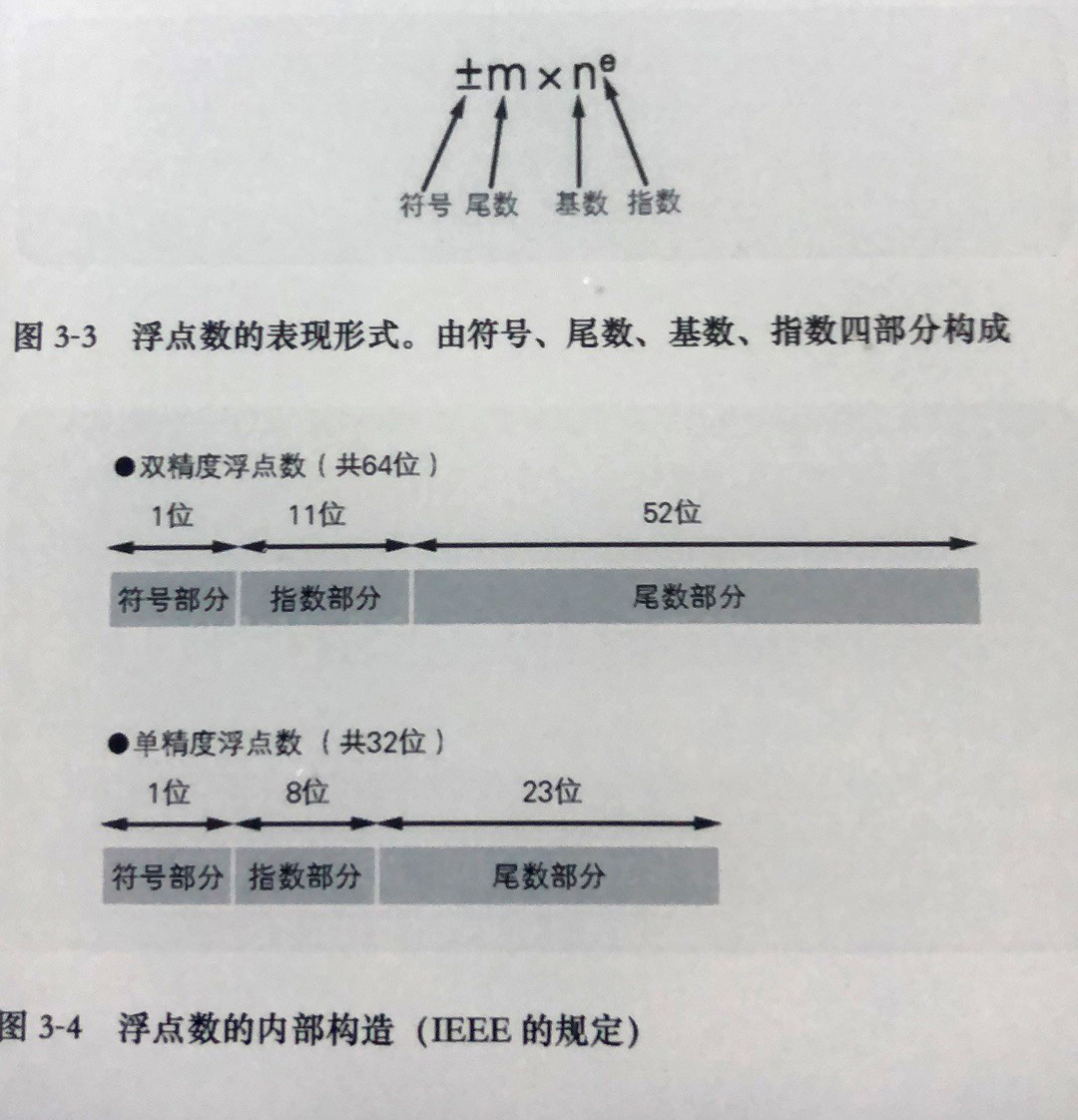
符号部分:是指使用一个数据位来表示数值的符号。和用二进制数来表示整数时的符号位时相同的
尾数部分:用的是“将小数点前面的值固定为1的正则表达式”(按照特定的规则来表达数据的形式即为正则表达式)
指数部分:用的则是“EXCESS系统表现”
3.正则表达式和EXCESS系统
尾数部分:
正则表达式:在二进制中,我们使用的是“将小数点前面的值固定为1的正则表达式”。具体来讲,就是将二进制数表示的小数左移或右移(这里是逻辑位移)数次后,整数部分的第1位变为1,第2位之后都变成0(这样是为了消除第2位以上的数位)。而且,第1位的1实际的数据中不保存。由于第1位必须是1,因此,省略该部分后就节省了一个数据位,从而也就可以表示更多的数据范围(虽不算太多)
单精度浮点数的正则表达式的具体例子如下:
| 1011.0011 | 原始数值 |
| 0001.0110011 | 右移使整数部分的第1位变成1 |
|
0001.01100110000000000000000 |
确保小数点以后的长度为23 |
| 01100110000000000000000 | 仅保留小数点后面的部分 |
指数部分:
EXCESS系统表现:通过将指数部分表示范围的中间值设为0,使得负数不需要用符号来表示,当指数部分是8位单精度浮点数时,最大值11111111 = 255的1/2,即011111111 = 127(小数部分舍弃)表示的是0,指数部分是11位双精度浮点数时,1111111111 = 2047的1/2,即011111111111 = 1023(小数部分舍弃)表示的是0。
单精度浮点数指数部分的EXCESS系统表现
| 实际的值(二进制数) | 实际的值(十进制数) | EXCESS系统表现(十进制数) |
| 11111111 | 255 | 128 =(255-127) |
| 11111110 | 254 | 127 =(254-127) |
| …… | …… | …… |
| 01111111 | 127 | 0 =(127-127) |
| 01111110 | 126 | -1 =(126-127) |
| …… | …… | …… |
| 00000001 | 1 | -126 =(1-127) |
| 00000000 | 0 | -127 =(0-127) |
在实际的程序中进行确认:
1 #include <stdio.h> 2 3 void main(void){ 4 float data; 5 unsigned long buff; 6 int i; 7 char s[34]; 8 9 //将0.75以单精度浮点数的形式存储在变量data中 10 data = (float)0.75; 11 12 //把数据复制到4字节长度的整数变量buff中以逐个提取出每一位。 13 memcpy(&buff,&data,4); 14 15 printf("%ld ",buff); 16 17 18 //逐个提取出每一位 19 for (i = 33; i >= 0; i--){ 20 if(i == 1|| i == 10){ 21 //加入破折号来区分符号部分,指数部分和尾数部分。 22 s[i] = '-'; 23 }else{ 24 //为各个字节赋值‘0’或者‘1’ 25 if(buff % 2 == 1){ 26 s[i] = '1'; 27 }else{ 28 s[i] = '0'; 29 } 30 buff /= 2; 31 } 32 } 33 s[34] = '�'; 34 35 //显示结果 36 printf("%s ",s); 37 38 getchar(); 39 40 }
输出结果:
1061158912 0-01111110-10000000000000000000000
该程序执行后,十进制数0.75用单精度浮点数来表示就变成了0-01111110-1000000000000000000000表示的就是(+1.5*2的-1次幂)。