动态查找之二叉树查找 c++实现

算法思想

二叉搜索树（又称二叉查找树或二叉排序树）BST树

二叉查找树

　　二叉查找树，也称二叉搜索树，或二叉排序树。其定义也比较简单，要么是一颗空树，要么就是具有如下性质的二叉树：

（1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2） 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3） 任意节点的左、右子树也分别为二叉查找树；

（4） 没有键值相等的节点。

二叉查找树的性质总结：　

a.二叉查找树还有一个性质，即对二叉查找树进行中序遍历，即可得到有序的数列。

​b.二叉查找树的查询复杂度，和二分查找一样，插入和查找的时间复杂度均为 O(logn) ，但是在最坏的情况下仍然会有 O(n) 的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡。

具体实现:

/****
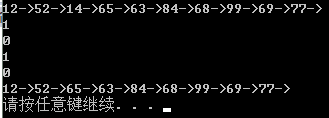
* BinarySortTree.
*
****/
#include"stdafx.h"
#include <iostream>
#include<queue>
using namespace std;
typedef struct node
{
    int elem;
    struct node* leftchild;
    struct node* rightchild;
}BitNode,*BinTree;
//insert binary tree function
BinTree Insert_BinaryTree(BinTree &bt,int key)
{
    if (bt == 0)
    {
        bt = new BitNode;
        bt->elem = key;
        bt->leftchild = 0;
        bt->rightchild = 0;
        return bt;
    }
    if (key < bt->elem)
    {
        bt->leftchild = Insert_BinaryTree(bt->leftchild,key);
    }
    else
    {
        bt->rightchild = Insert_BinaryTree(bt->rightchild, key);
    }
    return bt;
}
//for one search binary tree function
int Search_BinaryTree(BinTree &bt,int key)
{
    if (bt == 0) return 0;
    if (bt->elem == key) return 1;
    
    if (key < bt->elem)
    {
        return Search_BinaryTree(bt->leftchild,key);
    }
    else
    {
        return Search_BinaryTree(bt->rightchild, key);
    }
}
// for another one search binary tree function
int Search_BinaryTree(BinTree &bt, int key, BitNode ** p, BitNode** pf)
{
    *p = bt;
    *pf = 0;
    while (*p != 0)
    {
        if ((*p)->elem == key)
            return 1;
        if ((*p)->elem > key)
        {
            *pf =*p;
            *p = (*p)->leftchild;
        }
        else
        {
            *pf = *p;
            *p = (*p)->rightchild;
        }
    }
    return 0;
}
//delete binary tree function
int Delete_BinaryTree(BinTree *bt,int key)
{
    BitNode *p=*bt;
    BitNode *pf=0;
    int findflag;
    if (bt == 0) return 0;
    findflag = Search_BinaryTree(*bt,key,&p,&pf);
    if (findflag == 0) return 0;
//删除的节点是叶子节点
    if (p->leftchild == 0 && p->rightchild == 0)
    {
        if (pf == 0)
        {
            delete bt;
            bt = 0;
            return 1;
        }
        if (p == pf->leftchild)
        {
            pf->leftchild = 0;
            delete p;
            p = 0;
            return 1;
        }
        else
        {
            pf->rightchild = 0;
            delete p;
            p = 0;
            return 1;
        }
    }
    //删除的节点只有一个子节点
    if (p->leftchild == 0)
    {
        if (pf = 0)
        {
            *bt = p->rightchild;
            delete p;
            return 1;
        }
        if(p==pf->leftchild)
        {
            pf->leftchild = p->rightchild;
            delete p;
            return 1;
        }
        else
        {
            pf->rightchild = p->rightchild;
            delete p;
            return 1;
        }
    }

    if (p->rightchild == 0)
    {
        if (p == pf->leftchild)
        {
            pf->leftchild = p->leftchild;
            delete p;
            return 1;
        }
        if (p == pf->rightchild)
        {
            pf->rightchild = p->leftchild;
            delete p;
            return 1;
        }
    }
    //3.删除的节点含有两个子节点
    BitNode * prf = p;
    BitNode * pr = p->rightchild;
    while (pr->leftchild != 0)
    {
        prf = pr;
        pr = pr->leftchild;
    }
    if(prf == p)
    {
        p->elem = pr->elem;
        prf->rightchild = pr->rightchild;
    }
    else
    {
        p->elem = pr->elem;
        prf->leftchild = pr->rightchild;
    }
    delete pr;
    return 1;

}

//print binary tree function
void printTree(BitNode * bt)
{
    queue<BitNode*> q;
    q.push(bt);
    while (!q.empty())
    {
        BitNode* p = q.front(); q.pop();
        if (p)
        {
            cout << p->elem << "->";
            q.push(p->leftchild);
            q.push(p->rightchild);
        }
    }
    cout << endl;
}
//test  function
int main()
{
    int a[10] = { 12, 52, 65, 84, 63, 14, 68, 69, 99,77 };

    // initialization and creat the Binary Sort Tree.
    BinTree bt = 0;
    for (int i = 0; i < 10; i++)
    {
        bt = Insert_BinaryTree(bt, a[i]);
    }
    printTree(bt);
    //search start.
    cout << Search_BinaryTree(bt, 14) << endl;
    cout << Search_BinaryTree(bt, 55) << endl;

    //delete start.
    cout << Delete_BinaryTree(&bt, 14) << endl;

    //search 14 again.
    cout << Search_BinaryTree(bt, 14) << endl;
    printTree(bt);
    system("pause");
    return 0;
}