1.直方图
用于计算图片特征,表达, 使得数据具有总结性, 颜色直方图对数据空间进行量化,好比10个bin
2. 聚类
类内对象的相关性高
类间对象的相关性差
常用算法:kmeans, EM算法, meanshift, 谱聚类(密度聚类), 层次聚类
kmeans聚类
选取k个类中心,随机选取
计算每个点跟k个类中心的位置
把数据点分配给距离最近的一个类中心
计算新的类中心-对该类中的所有点取均值
类中心数K的选取
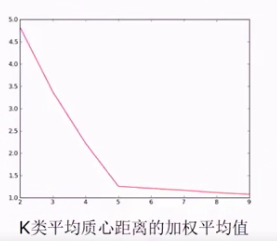
K类平均质心的距离加权平均值, 当k=5时的斜率发生变化,我们可以选取5作为分类的个数
kmeans ++ 半随机(初始点的选取)
第一类中心 - 随机选取
记D(x) 为数据点x距离最近的聚类中心的距离
选取下一个聚类中心, 选取的概率正比于D(x) ^ 2
以此类推,到第k个
量化颜色直方图
聚类颜色直方图: 使用聚类算法对像素点颜色向量进行聚类, 单元由聚类中心代表
3. 边缘检测
像素明显变化的区域, 具有丰富的语义信息
用途: 物体识别,几何视角变化
定义: 像素函数快速变化的区域, 一阶导数的极值区域,二阶导数的0点位置
步骤:
先高斯去噪,再使用一阶导数获取极值
公式: 对x方向进行求导 б 表示的是标准差 对y方向进行求导

梯度幅值/强度
hx(x,y)^ 2 + hy(x, y) ^ 2
梯度(增加最快)方向
arctan(hy(x, y)/ hx(x, y))
4. 兴趣点/关键点
稳定局部
特点: 可重复性,显著性
抗图片变化
外貌变化(亮度,光照)
几何变化(平移, 选择,尺度)
5.Harris角点
一种显著点:在任何方向上移动小观察窗,导致大的像素变动
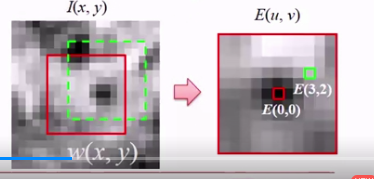
E(u, v) = ΣW(x, y)[I(x+u, y+v)-I(x, y)] ^2
W(x, y)是高斯函数进行加权的, x,y表示当前位置, u和v表示移动了的位置
6.斑点(Blob)
拉普拉斯梯度:一阶导数极值点 - 二阶导数零点
梯度/边缘可以通过查找:二阶导数接近零, 一阶导数足够大
对噪声很敏感, 需要先做高斯平滑
公式: Δf = δ2f / δ2x + δ2f / δ2y 对x求二阶导, 对y方向求二阶导
斑点是找拉普拉斯的极值
边缘是找拉普拉斯的零值
7.SIFT
SIFT特征计算
计算高斯差分(DoG)尺度空间,获取极值点
特征点处理: 位置插值, 去除低对比度点, 去除边缘点
方向估计: 2*2网格, 8个方向,获得最高值为关键点的主方向,特征点方向归一化,即所有方向为同一方向
描述子提取: 在旋转坐标上采样16*16的像素窗, 4*4网格,8方向直方图,总共178维
8.纹理特征
HOG(方向梯度直方图)
梯度幅值,方向 s = sqrt(sx^2 + sy^2)
Block 拆分
16*16的block 步长是8, 包含2*2个cell, 每个cell8*8, 9个方向
积累梯度幅值,使用位置高斯加权,使用相邻bin线性插值
64&128的维度图:7*15 * (2*2) * 9 = 3780
LBP(局部二值模式)
将每个像素点与周围点大小半径比较,半径R的圆上,均匀采样P个点,根据赫值大小,量化为0或1