问题:LSTM的输出值output和state是否是一样的
1. rnn.LSTMCell(num_hidden, reuse=tf.get_variable_scope().reuse) # 构建单层的LSTM网络
参数说明:num_hidden表示隐藏层的个数,reuse表示LSTM的参数进行复用
2.rnn.DropoutWrapper(cell, output_keep_prob=keep_prob) # 表示对rnn的输出层进行dropout
参数说明:cell表示单层的lstm,out_keep_prob表示keep_prob的比例,即保存的比例
3. tf.contrib.rnn.MultiRNNCell([create_rnn_layer for _ in range(num_lstm)], state_is_tuple=True) # 构建多层的LSTM网络
参数说明:[create_rnn_layer for _ in range(num_lstm)]构建LSTM的列表,state_is_tuple表示需要经过重叠
4.mlstm_cell.zero_state(batch_size, tf.float32) 表示进行state的初始值,维度为batch_size * num_hidden
参数说明:batch_size表示输入图片的个数,tf.float32表示类型
5.(output, state) = mlstm_cell(X[:, timestamp, :], state) 表示每一次输入获得输出值和state,
参数说明:X[:, timestamp, :] 表示X的输入值,state表示上一层的输出值
6.np.asarray(s) # 在改变数据类型的同时将不复制原来的数据
参数说明:s表示输入的列表
7.plt.bar(bar_index, pre[0], width=20, aligh='center') # 做直方图
参数说明:bar_index表示x轴的位置,pre[0] 表示y轴的大小, width表示宽度,aligh表示直方图的对其方式
代码说明:
数据说明:mnist数据集,将一张图片分为28次输入,每次输入为一行28个像素点,从上到下输入
模型说明:模型的隐藏层的参数为256层,每次迭代输入的state的大小为_batch_size * hidden_num, 模型的层数为2层LSTM
代码主要是由三部分组成:
第一部分:进行模型的训练和预测
第二部分:选取5张图片,打印模型的outputs输出层的大小
第三部分:选择一张图片,输出outputs,使用sess.run() 获得w和b的实际值,循环outputs,使用sess.run(tf.nn.sotfmax(tf.matmul(output, w) + b)), 对每一层的输出概率做图,一共是28层
第一部分:
第一步:mnist数据集的输入
第二步:超参数的设置,学习率,每次输入的大小,输入的次数,隐藏层的个数,分类的类别, LSTM的层数
第三步:使用tf.placeholder()定义输入,包括_X, Y, batch_size, keep_prob, 同时对_X进行维度的变换,使得其变成[-1, 28, 28]
第四步:定义create_rnn_layer() 用于生成单层的rnn网络,rnn.LSTMCell构造单层LSTM网络, rnn.DropoutWrapper进行dropout层的定义
第五步:mlstm_cell = tf.contrib.rnn.MultiRNNCell进行多层LSTM的网络构建
第六步:使用mlstm_cell.zero_state(batch_size, dtype=tf.float32) # 进行初始state的构建
第七步:对timestamp_size进行循环,如果循环次数大于1,就使用tf.get_variable_scope().reuse_variables() 进行参数的复用, (output, state) = mlstm_cell(X[:, timestamp, :], state), 将获得的output添加到outputs中
第八步:取最后一个outputs作为最后的结果输出,大小为[?, 256]
第九步:构造W和b参数进行最后结果的预测,即将256转换为10分类
第十步:使用tf.nn.softmax(tf.matmul(h_output, W) + b) 获得输出的softmax概率值
第十一步:使用-tf.reduce_mean(y * tf.log(y_pre)) # 构造损失函数
第十二步:使用tf.train.Adaoptimer() 构造降低损失值的train_op
第十三步:使用tf.equal 和tf.reduce_mean构造准确率
第十四步:进行循环操作,使用mnist.train.next_batch(_batch_size)获得数据
第十五步:sess.run(train_op) 进行降低损失值的操作,迭代200次打印训练集的准确率, 迭代的epoch值
第十六步:打印测试集的训练结果,
import tensorflow as tf import numpy as np from tensorflow.contrib import rnn from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt # 第一步数据读取 mnist = input_data.read_data_sets('/data', one_hot=True) # 第二步:超参数设置 lr = 1e-3 # 学习率的设置 input_num = 28 timestamp_size = 28 lstm_num = 2 num_hidden = 256 num_classes = 10 # 第三步:输入参数的初始化操作 _X = tf.placeholder(tf.float32, [None, 784]) y = tf.placeholder(tf.float32, [None, num_classes]) batch_size = tf.placeholder(tf.int32, []) keep_prob = tf.placeholder(tf.float32, []) # 改变输入的维度,变成N*28*28 X = tf.reshape(_X, [-1, timestamp_size, input_num]) # 第四步:构造函数创建多层的LSTM def create_rnn_layer(): cell = rnn.LSTMCell(num_hidden, reuse=tf.get_variable_scope().reuse) return rnn.DropoutWrapper(cell, output_keep_prob=keep_prob) # 第五步:使用tf.contrib.rnn.MultiRNNCell mlstm_cell = tf.contrib.rnn.MultiRNNCell([create_rnn_layer() for _ in range(lstm_num)], state_is_tuple=True) # 第六步:使用mlstm_cell.zero_state构造初始化的state init_state = mlstm_cell.zero_state(batch_size, dtype=tf.float32) # 第七步:对每一个输入的数据进行迭代,获得state,并作为下一次的输入,重新输入到LSTM网络中,最后的输出即为预测结果 outputs = list() state = init_state with tf.variable_scope('RNN'): for timestamp in range(timestamp_size): if timestamp > 0: tf.get_variable_scope().reuse_variables() (output, state) = mlstm_cell(X[:, timestamp, :], state) outputs.append(output) # 第八步:使用最后一个结果,作为输出值 h_state = outputs[-1] # 第九步:定义W和b,用于将LSTM的输出变成预测的输出 W = tf.Variable(tf.truncated_normal([num_hidden, num_classes], stddev=0.1), dtype=tf.float32) b = tf.Variable(tf.constant(0.1, shape=[num_classes]), dtype=tf.float32) # 第十步:使用tf.matmul进行线性变换,使用softmax将结果转换为概率值 y_pre = tf.nn.softmax(tf.matmul(h_state, W) + b) # 第十一步:使用tf.log(y_pre) * y 获得交叉熵损失函数 loss = -tf.reduce_mean(tf.log(y_pre) * y) # 第十二步:使用tf.train.Adam降低损失值 train_op = tf.train.AdamOptimizer(lr).minimize(loss) # 第十三步:使用tf.equal和tf.reduce_mean 获得准确率 correct_pred = tf.equal(tf.argmax(y_pre, 1), tf.argmax(y, 1)) accurracy = tf.reduce_mean(tf.cast(correct_pred, 'float')) # 进行初始化操作 sess = tf.Session() sess.run(tf.global_variables_initializer()) # 一个batch_size的大小 _batch_size = 64 for i in range(2000): # 循环,第十四步:获得一个batch的数据 batch = mnist.train.next_batch(_batch_size) # 第十五步:训练train_op, keep_prob等于0.5, 当迭代次数为200时,打印训练的准确度 if i % 200 == 0: train_accur = sess.run(accurracy, feed_dict={_X:batch[0], y:batch[1], keep_prob:1.0, batch_size:_batch_size}) print('train epoch %d train iteration %d train accur %g'%(mnist.train.epochs_completed, i, train_accur)) sess.run(train_op, feed_dict={_X:batch[0], y:batch[1], keep_prob:0.5, batch_size:_batch_size}) # 第十六步:打印测试集的准确率 print('test accur %g'%(sess.run(accurracy, feed_dict={_X:mnist.test.images, y:mnist.test.labels, keep_prob:1.0, batch_size:mnist.test.images.shape[0]})))
第二部分:输入_batch_size = 5 的类别值,打印outputs的维度
第一步:定义_batch_size = 5
第二步:使用mnist.train.next_batch(_batch_size) 获得X_batch, y_batch
第三步:_outputs, _state = sess.run([outputs, state], feed_dict={}) 获得outputs的结果
第四步:打印outputs的维度, 使用print(np.asarray(outputs).shape)
# 第二部分:打印outputs的维度 # 第一步:定义输入的_batch_size _batch_size = 5 # 第二步:获得mnist中Train的数据 X_batch, y_batch = mnist.train.next_batch(_batch_size) # 第三步:使用sess.run获得,outputs的实际值 _outputs, state = sess.run([outputs, state], feed_dict={_X:X_batch, y:y_batch, keep_prob:1.0, batch_size:_batch_size}) # 第四步:打印_outputs的维度 print('outputs shape=', np.asarray(_outputs).shape)
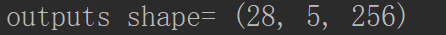
outputs的维度第一个维度,表示28个输出,5表示5张图片,256表示隐藏层的个数
第三部分:抽取一张图片,做出每一个输出的概率直方图
第一步:获得一张图片,将其维度转换为[-1, 784] 即二维,获得图片对应的标签,将其维度转换为[-1, 10] 即二维
第二步:使用sess.run(outputs, feed_dict) 获得这张图片的outputs输出值
第三步:使用sess.run获得W和b,并赋值为h_w和h_b
第四步:循环outputs,使用tf.nn.softmax(tf.matmul(x_batch, h_w) + h_b)
第五步:画直方图,plt.bar(bar_index, pro[0], width=20, align='center') bar_index等于np.arange(num_classes), plt.axis('off')
# 第三部分:对每一部分的输出值进行概率的作图 # 第一步:图片的输入,即将图片的维度进行变换,对应标签的输入,对图片的标签进行维度变换 image = mnist.train.images[4] image.shape = [-1, 784] image_size = image.reshape([28, 28]) plt.imshow(image_size, cmap='gray') plt.show() y_labels = mnist.train.labels[4] y_labels.shape = [-1, num_classes] # 第二步:使用sess.run(outputs)获得outputs的输出值 output_array = np.array(sess.run(outputs, feed_dict={_X:image, y:y_labels, keep_prob:1.0, batch_size:1})) # 对outputs转换为二维类型,即[28, 1, 256] 转换为[28, 256] output_array.shape = [28, 256] # 第三步:使用sess.run获得W和b的实际值 h_W = sess.run(W, feed_dict={_X:image, y:y_labels, keep_prob:1.0, batch_size:1}) h_b = sess.run(b, feed_dict={_X:image, y:y_labels, keep_prob:1.0, batch_size:1}) # 构建bar_index的X轴坐标 bar_index = np.arange(num_classes) plt.figure() for i in range(output_array.shape[0]): plt.subplot(4, 7, i+1) # 将[1, 256]重新转换为[1, 256]做一个维度的验证 X3_h_state = output_array[i, :].reshape([-1, num_hidden]) # 第四步:使用tf.nn.softmax将输出值转换为各个类别的概率值 pre = sess.run(tf.nn.softmax(tf.matmul(X3_h_state, h_W) + h_b)) # 第五步:画直方图操作 plt.bar(bar_index, pre[0], width=0.2, align='center') plt.axis('off') plt.show()
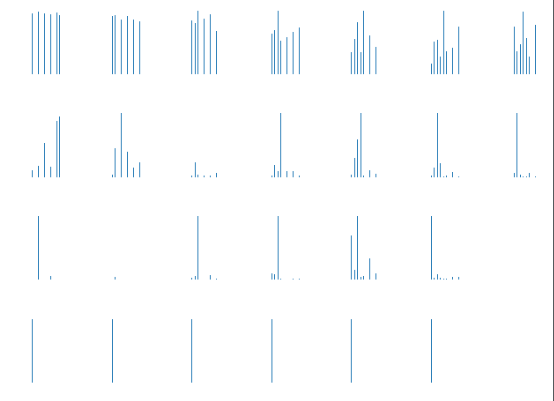
最后几次的预测结果,主要是以0为最终的结果