主成分分析:
用途:降维中最常用的一种方法
目标:提取有用的信息(基于方差的大小)
存在的问题:降维后的数据将失去原本的数据意义
向量的内积:A*B = |A|*|B|*cos(a) 如果|B| = 1,那么A*B = |A| * cos(a) 即在B的方向上对A做投影

基变化: 如果向量为(3, 2)那么它可以有(1, 0)和(0, 1)一组基进行表示,这两个基是正交的

在基变化过程中,每一个基都是正交的即线性无关
数据与第一个基进行内积,形成一个新的分量,数据与第二个基做内积,形成第二个分量,由于基是正交的,而内积表示的是投影,因此这两个分量也是正交的
即 1/m ai.dot(bi) = 0。
方差:变量的方差越大,其分散程度也就越大,方差 (ai-ui).dot((ai-ui).T) ui表示的是样本的均值
协方差:两个向量的内积,协方差越小,表示两个向量越不相似cov(a, b) = 1/m*(a.dot(b.T))
引入协方差的目的:
如果单纯只看变化后的方差大小,那么求得的基可能都在方差最大的方向附件进行徘徊,因为我们为了使变换后的特征尽可能的表示原始信息,我们使得变化后的特征是正交的情况,即特征之间线性无关,协方差cov=0
结合上述的两个条件:第一:变换后的矩阵的方差最大1/m ai.dot(ai.T)
第二:变换后的矩阵的协方差等于0 1/m ai.dot(bi.T)
我们引入了协方差矩阵,协方差矩阵对角线是方差,非对角线上是协方差
公式: 1/m X.dot(X.T)
1/m * Y.dot(Y.T) = 1/m PX.dot((PX).T) = 1/m(P* X * X^T * P^T)
令上面的式子中的 X*X^T等于C,那么上面的式子就是 1/m * Y.dot(Y.T) = 1/m(P* C * P^T)
我们需要使得1/m * Y.dot(Y.T) 满足上述两个条件,即对C做一个对角化变化,使得变化后的矩阵对角线上的表示方差(从大到小排列), 非对角线上等于0

这个问题前人已经研究了很透,即上述变化的P就是C的特征向量,而C等于X*X^T
我们只需要求得X*X^T的特征向量即可
上述的过程的实现步骤:
1.对特征进行标准化
2.去均值
3.求协方差矩阵 X*X^T
4.协方差矩阵的特征向量
5.使用前几维的特征向量与特征进行内积,实现特征降维
代码:
第一步:导入数据, 进行列名赋值
第二步:提取特征和标签
第三步:对每一个特征进行物体类别画直方图,研究不同变量对特征分布的影响
第四步:对样本特征进行标准化操作
第五步:对样本去均值并构造协方差矩阵X.dot(X.T)
第六步:对构造好的协方差矩阵求特征值和特征向量
第七步:将求得的特征值和特征向量进行组合, 对组合的特征进行排序操作,将排序后的特征进行使用np.cumsum对特征值进行加和
第八步:使用条形图和步进图对特征值和加和后的特征进行作图操作
第九步:选取前两个特征向量与标准化后的特征进行内积操作,获得降维后的特征
第十步:对降维后的特征画出散点图
import numpy as np import pandas as pd import matplotlib.pyplot as plt # 第一步 数据读取 data = pd.read_csv('iris.data') data.columns = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'classes'] # 第二步 提取特征 X = data[['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid']].values y = data['classes'].values feature_names = ['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid'] label_names = data['classes'].unique() # 第三步 对每一个特征的样品类别做直方图 for feature in range(len(feature_names)): plt.subplot(2, 2, feature+1) for label in label_names: plt.hist(X[y==label, feature], bins=10, alpha=0.5, label=label) plt.legend(loc='best') plt.show()
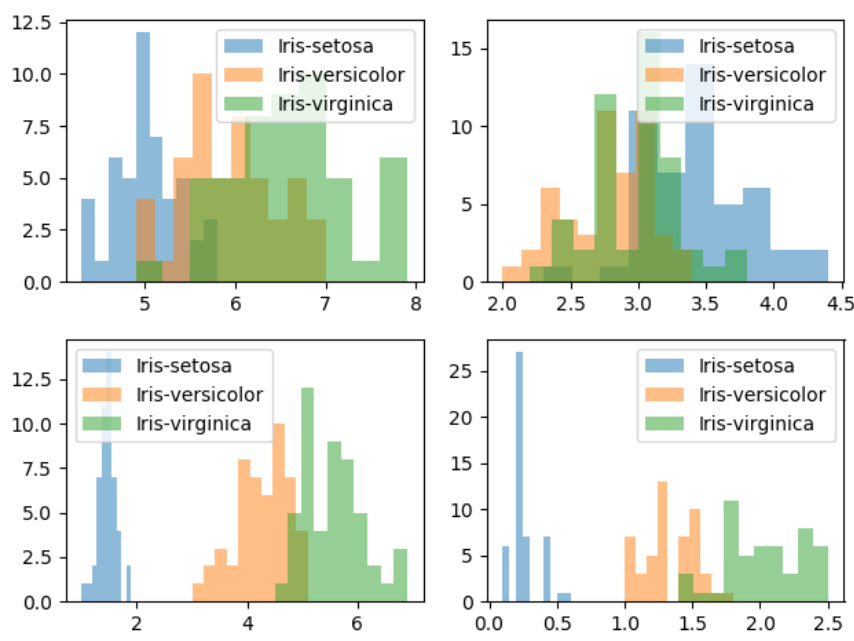
不同变量对类别分布的影响
# 第四步 对特征进行标准化操作 from sklearn.preprocessing import StandardScaler std_feature = StandardScaler().fit_transform(X) # 第五步 对特征去除均值, 并构造协方差矩阵, 也可以使用np.conv进行构造 mean_fea = std_feature.mean(axis=0) cov_matrix = (std_feature - mean_fea).T.dot(std_feature-mean_fea) # 第六步 使用np.linalg.eig 求出协方差矩阵的特征值和特征向量 eig_val, eig_vector = np.linalg.eig(cov_matrix) # 第七步:我们将特征值和特征向量进行组合 eig_paries = [(eig_val[j], eig_vector[:, j]) for j in range(len(eig_val))] # 获得对组合的特征值进行排序,获得重要性的占比 sum_val = np.sum(eig_val) feature_importance = [eig_v[0]/sum_val * 100 for eig_v in sorted(eig_paries, key=lambda x:x[0], reverse=True)] print(feature_importance) # 使用np.cumsum进行两两的前后加和 su_feature_importance = np.cumsum(feature_importance) # 第八步:对特征重要性进行作图操作 figure = plt.figure(figsize=(8, 6)) plt.bar(range(4), feature_importance, align='center', label='identity explain variance', alpha=0.5) # plt.step表示的是步进图, where表示的线条的表示方式 plt.step(range(4), su_feature_importance, where='mid', label='cumidentity explain variance') plt.xlabel('PC component') plt.ylabel('variance importance') plt.show()
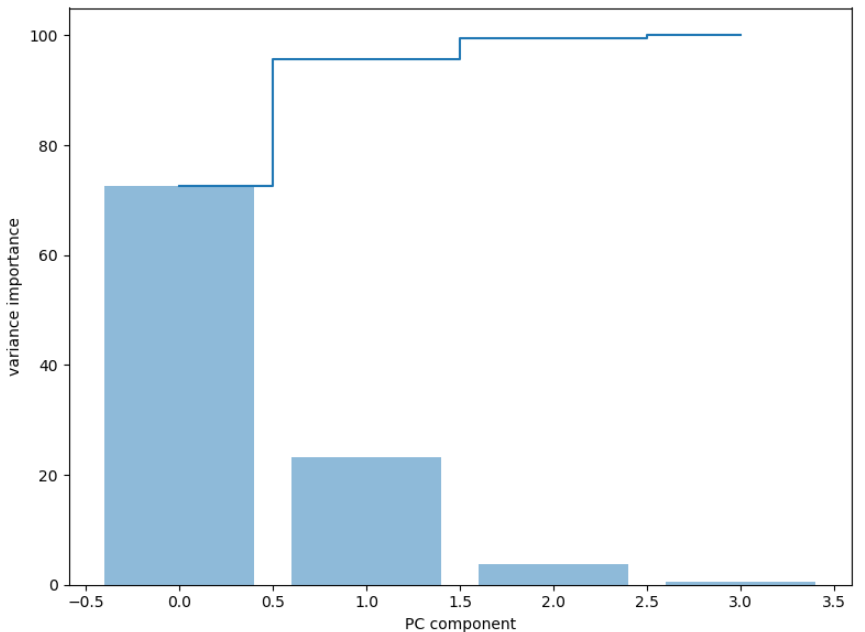
特征值重要比例图
# 第九步:使用前两个特征向量进行矩阵的变换 eig_vector_two = np.vstack([eig_paries[0][1], eig_paries[1][1]]) trans_std_X = std_feature.dot(eig_vector_two.T) # 第十步: 对变化后的数据进行画图操作 figure = plt.figure(figsize=(8, 6)) for label, c in zip(label_names, ['red', 'green', 'black']): plt.scatter(std_feature[y==label][:, 0], std_feature[y==label][:, 1], c=c, label=label, alpha=0.6, s=20) leg = plt.legend(loc='best') leg.get_frame().set_alpha(0.6) plt.xlabel(feature_names[0]) plt.ylabel(feature_names[1]) plt.show() figure = plt.figure(figsize=(8, 6)) for label, c in zip(label_names, ['red', 'green', 'black']): plt.scatter(trans_std_X[y==label][:, 0], trans_std_X[y==label][:, 1], c=c, label=label, alpha=0.6, s=20) leg = plt.legend(loc='best') leg.get_frame().set_alpha(0.6) plt.xlabel('PC1') plt.ylabel('PC2') plt.show()


原始特征图 降维后的特征图