1.from sklearn.processing import LabelEncoder 进行标签的代码编译
首先需要通过model.fit 进行预编译,然后使用transform进行实际编译
2.from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA 从sklearn的线性分析库中导入线性判别分析即LDA
用途:分类预处理中的降维,做分类任务
目的:LDA关心的是能够最大化类间区分度的坐标轴
将特征空间(数据中的多维样本,将投影到一个维度更小的K维空间,保持区别类型的信息)
监督性:LDA是“有监督”的,它计算的是另一个类特定的方向
投影:找到更适用的分类空间
与PCA不同: 更关心分类而不是方差(PCA更关心的是方差)

如图所示,找到合适的方向投影后的数据更加的分散
LDA的数据原理:
目标找到投影:y = w^T * x ,我们需要求解出w

LDA的第一个目标是使得投影后两个类别之间的距离越大越好,使用的判别依据,是投影后两个类别的中心点的距离越大越好,即均值u1^ - u2^
第一步:求出当前均值和投影后的均值
J(W) = |w^T(u1 - u2)| # 计算投影以后的两个类别中心位置之差

LDA的第二个目标是使得投影后的类别之间的距离越来越小,从图一中我们可以看出,只讨论类别之间的距离是不够的, 同类之间的距离使用单个类别的数据到类别中心之差来表示,值越大,同类数据越分散,值越小,同类数据越集中,我们需要使得这个值的大小越小越好
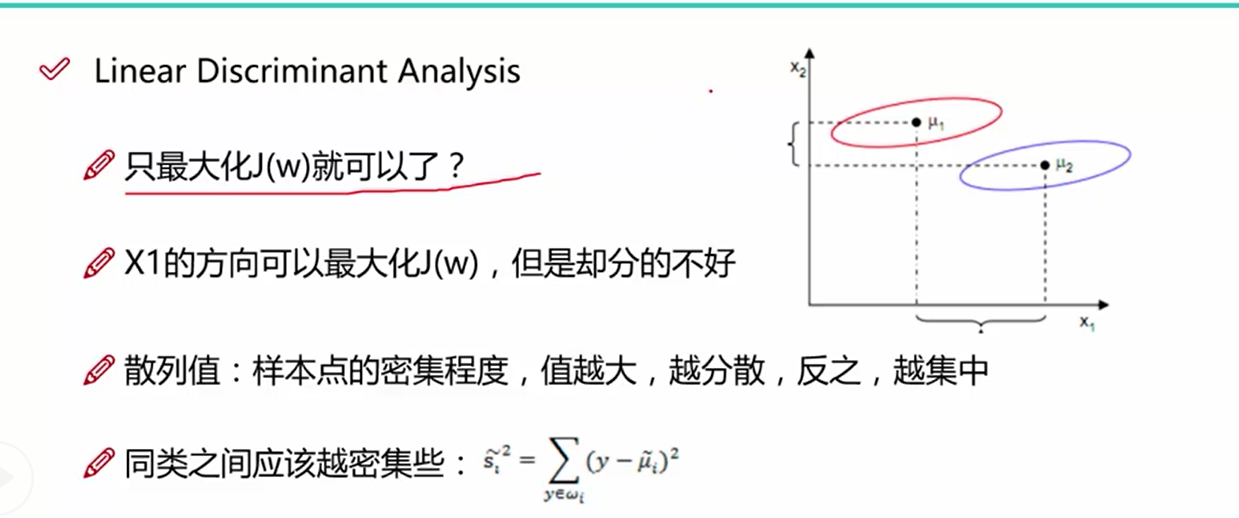
根据上面两个目标函数,我们做一个组合, 分子使用类间距离, 分母使用类内距离,求得组合后的最大值

该图表示的是最终的目标函数(类间距离/类内距离),这里的类内散布矩阵:通过同种类别数据-该类别的均值之差进行加和后求得
求得类间距离的散步矩阵

上述的目标矩阵就是我们求解的方程,我们需要求得其最大值
构造拉格朗日方程, 我们对分母进行缩放,使得w^TSw*w = 1, 作为限制条件
cw = w^T*SB*w - a(w^T*Sw*w-1) --构造的拉格朗日方程
cw/dw = w^T*SB*w - a(w^T*Sw*w-1) / dw 对上述方程使用dw进行求导,求偏导等于零求最大值
2SB*w - 2*a*Sw * w = 0
a * w = Sw^-1*SB*w ---- a*w = A*w
w是Sw^-1*SB的特征向量

代码:自己自行的编写
第一步:读取数据
第二步:提取样本变量和标签
第三步:对标签进行数字映射,使用LableEncoder
第四步:计算类内散列矩阵Sw sum((x-ui).dot((x-ui).T))
第五步:计算类间散列矩阵SB sum(n*(ui-u).dot(ui-u)) ui表示每一类样本的均值, u表示所有样本的均值
第六步:计算Sw^-1*SB的特征向量,即w,如果我们投影的维度是2,使用np.vstack, 将求得的特征向量的第一列和第二列数据进行拼接
第七步:将二维的w和X特征进行点乘操作, 获得变化后的二维特征
第八步:进行画图操作
import pandas as pd import numpy as np import matplotlib.pyplot as plt # 第一步数据载入 data = pd.io.parsers.read_csv(filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None, names=['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm', 'names'], sep=',',) data.dropna(how='all', inplace=True) # 第二步提取数据的X轴和y轴信息 feature_names = ['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm'] X = data[feature_names].values y = data['names'].values # 第三步 使用Label_encoding进行标签的数字转换 from sklearn.preprocessing import LabelEncoder model = LabelEncoder().fit(y) y = model.transform(y) + 1 labels_type = np.unique(y) # 第四步 计算类内距离Sw Sw = np.zeros([4, 4]) # 循环每一种类型 print(labels_type) for i in range(1, 4): xi = X[y==i] ui = np.mean(xi, axis=0) sw = ((xi - ui).T).dot(xi-ui) Sw += sw print(Sw) # 第五步:计算类间距离SB SB = np.zeros([4, 4]) u = np.mean(X, axis=0).reshape(4, 1) for i in range(1, 4): n = X[y==i].shape[0] u1 = np.mean(X[y==i], axis=0).reshape(4, 1) sb = n * (u1 - u).dot((u1 - u).T) SB += sb # 第六步:使用Sw^-1*SB特征向量计算w vals, eigs = np.linalg.eig(np.linalg.inv(Sw).dot(SB)) # 第七步:取前两个特征向量作为w,与X进行相乘操作,相当于进行了2维度的降维操作 w = np.vstack([eigs[:, 0], eigs[:, 1]]).T transform_X = X.dot(w) # 第八步:定义画图函数 labels_dict = data['names'].unique() def plot_lda(): ax = plt.subplot(111) for label, m, c in zip(labels_type, ['*', '+', 'v'], ['red', 'black', 'green']): plt.scatter(transform_X[y==label][:, 0], transform_X[y==label][:, 1], c=c, marker=m, alpha=0.6, s=100, label=labels_dict[label-1]) plt.xlabel('LD1') plt.ylabel('LD2') # 定义图例,loc表示的是图例的位置 leg = plt.legend(loc='upper right', fancybox=True) # 设置图例的透明度为0.6 leg.get_frame().set_alpha(0.6) #坐标轴上的一簇簇的竖点 plt.tick_params(axis='all', which='all', bottom='off', left='off', right='off', top='off', labelbottom='on', labelleft='on') # 表示的是坐标方向上的框线 ax.spines['top'].set_visible(False) ax.spines['bottom'].set_visible(False) ax.spines['left'].set_visible(False) ax.spines['right'].set_visible(False) plt.tight_layout() plt.grid() plt.show() plot_lda()

我们使用Sklearn自带的程序进行操作
第一步:读取数据
第二步:提取特征
第三步:对标签做数字映射,使用的是LabelEncoder
第四步:使用from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
第五步:结果进行画图
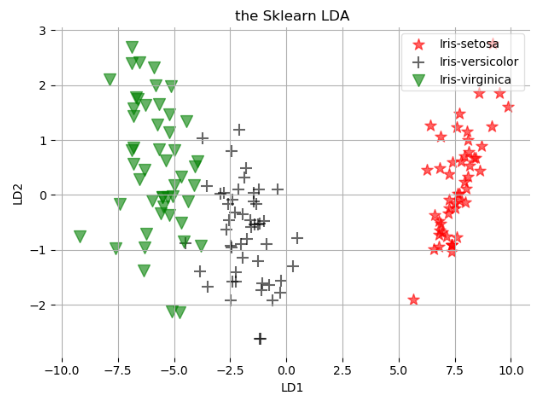
import pandas as pd import numpy as np import matplotlib.pyplot as plt # 第一步数据载入 data = pd.io.parsers.read_csv(filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None, names=['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm', 'names'], sep=',',) data.dropna(how='all', inplace=True) # 第二步提取数据的X轴和y轴信息 feature_names = ['sepal length in cm', 'sepal width in cm','petal length in cm', 'petal width in cm'] X = data[feature_names].values y = data['names'].values # 第三步 使用Label_encoding进行标签的数字转换 from sklearn.preprocessing import LabelEncoder model = LabelEncoder().fit(y) y = model.transform(y) + 1 labels_type = np.unique(y) # 第四步 建立LDA模型 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA model = LDA(n_components=2) sklearn_x = model.fit_transform(X, y) # 第五步进行画图操作 def plot_lda_sklearn(X, title): ax = plt.subplot(111) for label, m, c in zip(labels_type, ['*', '+', 'v'], ['red', 'black', 'green']): plt.scatter(X[y==label][:, 0], X[y==label][:, 1], c=c, marker=m, alpha=0.6, s=100, label=labels_dict[label-1]) plt.title(title) plt.xlabel('LD1') plt.ylabel('LD2') leg = plt.legend(loc='upper right', fancybox=True) leg.get_frame().set_alpha(0.6) plt.tick_params(axis='all', which='all', bottom='off', left='off', right='off', top='off', labelbottom='on', labelleft='on') ax.spines['top'].set_visible(False) ax.spines['bottom'].set_visible(False) ax.spines['left'].set_visible(False) ax.spines['right'].set_visible(False) plt.tight_layout() plt.grid() plt.show() plot_lda_sklearn(sklearn_x, 'the Sklearn LDA')