机器学习入门-K-means算法

无监督问题，我们手里没有标签

聚类：相似的东西聚在一起

难点：如何进行调参

K-means算法 

          需要制定k值，用来获得到底有几个簇，即几种类型

          质心：均值，即向量各维取平均值

          距离的度量： 欧式距离和余弦相似度

         优化目标： min∑∑dist(ci, xi)   即每种类别的数据到该类别质心距离的之和最小

                               1-k x

      

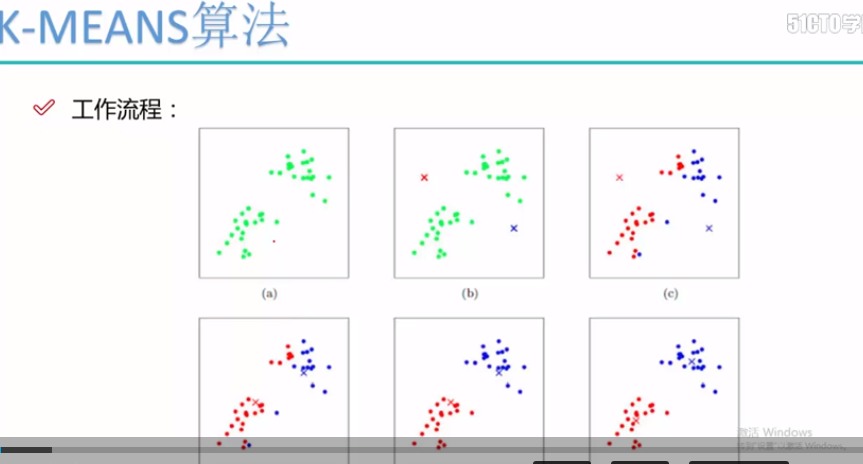
根据上述的工作流程：

                     第一步：随机选择两个初始点，类别的质心点(图二)

                     第二步： 根据所选的质心点，根据欧式距离对数据进行分类(图三)

                     第三步：求得分类后的每个类别的质心(图四)

                     第四步： 根据所选的质心点，根据欧式距离对数据进行分类(图五)

                     第五步：求得分类后的每个类别的质心(图五)

                     ....  一直到分类的数据类别不发生变化为止

优势：简单，快速，适用于常规数据集，分布较为规则的数据集

劣势：

          K值难确定

          复杂度与样本数据呈线性关系

         不太适用于不规则的数据

 我们使用sklearn来实现kmeans代码，使用silhouette_score轮廓系数来作为评估

第一步：读入数据

第二步：提取特征列

第三步：建立kmeans模型和训练

第四步：使用.grouby计算每一种类别的聚类中心，即求平均

第五步：使用scatter_matrix 画出两个变量关系的散点图

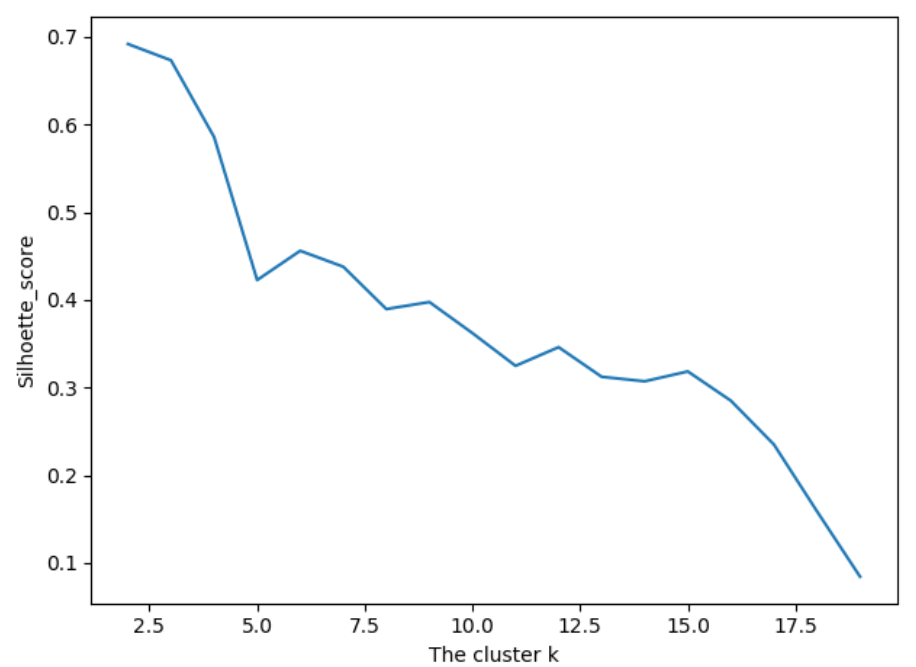
第六步：使用sihouette_score 轮廓系数来比较不同数目的聚类簇的结果影响

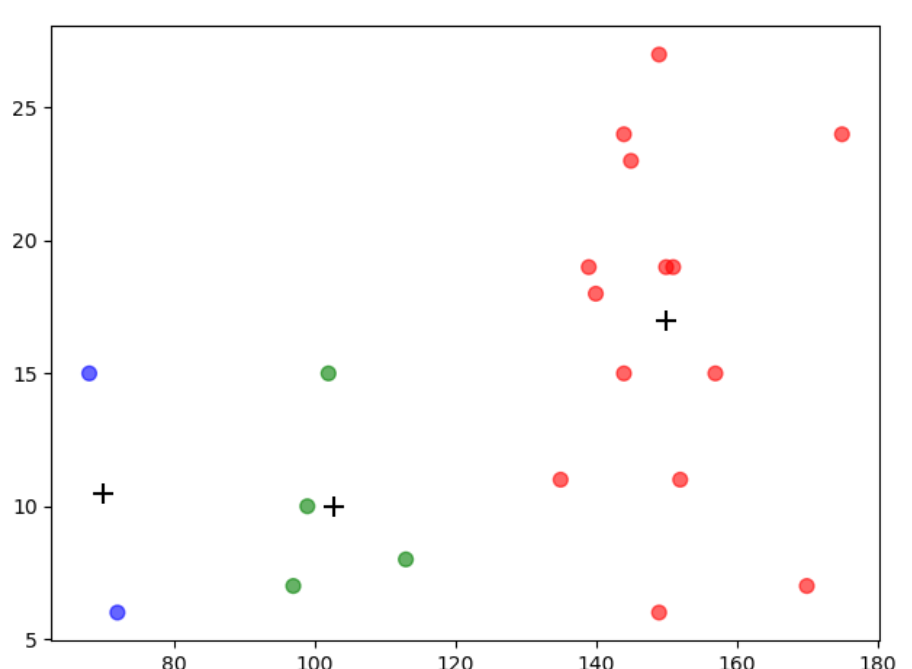
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


# 1.读入数据
data = pd.read_csv('data.txt', sep=' ')

# 2.提取特征
X = data[['calories', 'sodium', 'alcohol', 'cost']]

# 3.建立Kmeans模型和训练
from sklearn.cluster import KMeans

model = KMeans(n_clusters=3).fit(X)
beer = data.copy()
beer['cluster3'] = model.labels_
# 根据分类结果，从小到大进行排序
beer = beer.sort_values(by=['cluster3'])

# 4. 使用groupby 计算出每一个聚类中心的质心点， 画散点图
centers = beer.groupby(by=['cluster3']).mean()
colors = np.array(['red', 'green', 'blue', 'yellow'])
plt.scatter(beer['calories'], beer['sodium'], c=colors[beer['cluster3']], s=50, alpha=0.6)
# 画出质心的位置
plt.scatter(centers.calories, centers.sodium, c='k', marker='+', s=100)
plt.show()

、

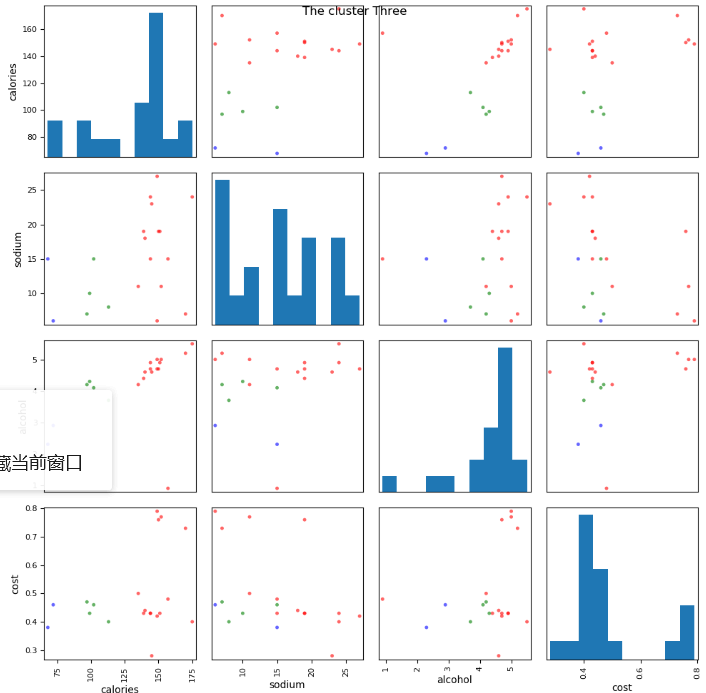
# 5. 使用scatter_matrix画出两两变量的关系图
from pandas.tools.plotting import scatter_matrix

scatter_matrix(beer[['calories', 'sodium', 'alcohol', 'cost']], s=50, alpha=0.6, c=colors[beer['cluster3']], figsize=(10, 10))
plt.suptitle('The cluster Three')
plt.show()

# 6.silhouette_score引入轮廓系数作为评估的标准
import sklearn

# k_cluster 从2-19,判断聚类的效果
scores = []
for i in range(2, 20):
    labels = KMeans(n_clusters=i).fit(X).labels_
    score = sklearn.metrics.silhouette_score(X, labels)
    scores.append(score)
    print(score)

plt.plot(list(range(2, 20)), scores)
plt.xlabel('The cluster k')
plt.ylabel('Silhoette_score')
plt.show()