[详解][学习笔记] 矩阵/矩阵乘法/矩阵快速幂/优化递推

 我是上网自学了很久,看了那么多博文还是看不懂...
然鹅 天无绝人之路 今天受 wudongchao 大佬 点拨 终于有所顿悟

带着自学无果的痛苦,我觉得写一篇学习笔记帮助和我一样蠢萌痛苦的人(其实基本就是总结摘抄)

矩阵/矩阵乘法/矩阵快速幂/优化递推

的通俗版内容(专业定义啊术语啥的我也不会)

本文大量盗取图片和内容,链接都附进去了.
由于本人懒,麻烦各位dalao看到的话私我上车补票(版权意识强的dalao请轻喷)

矩阵

矩阵(Matrix)是把一堆数字填在矩形表格中(所以叫矩阵?),就像:

这是个m行n列的矩阵,这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

 然后顺带提一下矩阵加法和减法,就对应元素加减就完事了...

矩阵乘法

矩阵乘法符合实数乘法的所有运算律 除了交换律 原因可以从运算方式看出

为了方便,我将三个矩阵如此区分:左边的因数矩阵叫作矩阵L (for left)  右边的因数矩阵叫作矩阵R (for right)  作为乘积的答案矩阵叫做矩阵A (for answer)

作为结果的矩阵A中的 (i,j)元 是左矩阵的第i行 和 右矩阵的第j列 对应元素分别相乘的和 (比较绕口: 对应元素的积的和)

左行右列

例:结果矩阵的(1,1)元=1*7+2*9+3*11=58

同理 具体每个元素如下: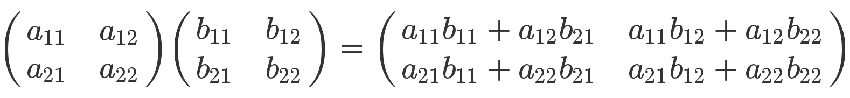

容易得出,只有在左矩阵的列数和右矩阵的行数相等时,算式才有意义
所以矩阵乘法要求三个个矩阵形如:
_Lxy * R_yz = A_xz 

结果矩阵的行列数取决于因数矩阵

矩阵乘法和矩阵快速幂

虽然挺简单的 但还是附一下矩阵乘法cpp代码

void _mat_mul(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int z) {
//L[x][y] * R[y][z] = A[x][z]
    long long cmp[LEN][LEN] = {0};
    for (int i = 1; i <= x; ++i)
        for (int j = 1; j <= z; ++j)
            for (int k = 1; k <= y; ++k)
                cmp[i][j] = (cmp[i][j] + L[i][k] * R[k][j]) % MOD;
    for (int i = 1; i <= x; ++i)for (int j = 1; j <= z; ++j)A[i][j] = cmp[i][j];
}

而矩阵快速幂只是在快速幂模板中 将乘法部分换成矩阵乘法(我调用了上面那个函数)

void _mat_mi(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int mi) {
// L[x][y] * R[y][y]^mi = A[x][y]
    int cmp[LEN][LEN];
    for (int i = 1; i <= x; ++i)for (int j = 1; j <= y; ++j)cmp[i][j] = L[i][j];
    while (mi > 0) {
        if (mi & 1)
            _mat_mul(cmp, Mat, cmp, x, y, y);
        mi >>= 1;
        _mat_mul(R, R, R, y, y, y);
    }
    for (int i = 1; i <= x; ++i)for (int j = 1; j <= y; ++j)A[i][j] = cmp[i][j];
}

 矩阵快速幂优化递推

Fibonacci

 终于来了!!! 虽然我也没学太好
总之慢慢写吧,欢迎交流

我们的目的是用乘法(快速幂)来优化加法
(不知道减法行不行?是不是系数写成负数就行了?感觉好像是的)

 首先我们得有一个递推式
以经典的斐波那契数列为例

F_(i) = F_(i-1) +F_(i-2) 

我们把相邻的两项写在一行(其实一列也行)

像这样: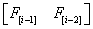

然后我们再构建一个能够自己乘自己很多次的矩阵
不难发现,符合这样条件的矩阵必须是"正方形"矩阵(好吧我好好说话:行数和列数一样的矩阵)
同时要能和我们上面列出来的矩阵相乘,
所以在这题中 必须是一个2x2的矩阵(想一想为什么不是1x1)

然后我们期望的 乘积矩阵 需要包含递推式的下一项,还要和我们前面构出来的矩阵长得差不多
原因是我们要反复类乘
比如: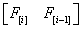

根据 矩阵乘法的要求 我们的算式应该长这样

 将F[i] 写成 F_[i-1] + F_[i-2] 后, 我们 根据矩阵乘法的运算法则 在矩阵中填上系数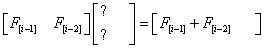

因为1 x F_[i-1] + 1 x F_[i-2] = F_[i-1] + F_[i-2] =  F_[i] (对应两项相乘的和)
所以我们填成这样:

同理,我们可以把剩下的空格填完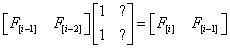

( 1 x F_[i-1] + 0 x F_[i-2] = F_[i-1] )

所以整个递推式是长这样的:

由于我们的 矩阵L 和 矩阵A 长得差不多,都可以写成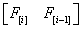

所以我们可以用这个式子递推

然鹅,我们用了矩阵这么高级的东西,可不只是把一个加法递推式变成一个乘法递推式而已

设想一下:我们已知 F_[2] 和 F_[1] 如果我们要得到 F_[N] 是不是需要把矩阵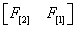 

乘很多次矩阵

所以我们容易得到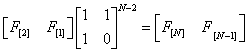

然后再套矩阵快速幂就好了

fib的矩阵快速幂源码

#define LEN 100
#define N 123
#define MOD 10000
// #define int long long
/**
 * LEN 矩阵边长
 * N   第N项
 * MOD 模数(因为太大会爆负)
 */

void _mat_mul(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int z);
void _mat_mi(int L[LEN][LEN], int R[LEN][LEN], int A[LEN][LEN], int x, int y, int mi);

int Fib[LEN][LEN], Mat[LEN][LEN] ;

signed main() {

    Fib[1][1] = Fib[1][2] = 1;

    Mat[1][1] = 1; Mat[1][2] = 1;
    Mat[2][1] = 1; Mat[2][2] = 0;

    if (N > 2)
        _mat_mi(Fib, Mat, Fib, 1, 2, N - 2);

    cout << Fib[1][1];

    return 0;

}

其实矩阵快速幂优化递推,完全都是套路!
只要把需要递推的相邻项写在两个矩阵 然后填中间的矩阵就好了
仔细思考矩阵乘法的运算方式...就完事了

如果有不清楚的评论或私我吧...写到这我也晕了