1.设计思想
根据以前的首尾相连的一维数组的最大子数组求出每一行的最大子矩阵,然后再两行相加,求出最大子矩阵,一直到所有的行相加,求出最大子矩阵。比较其中最大的子矩阵值,最后输出最大子矩阵和的值。
2.源程序
#include<iostream> #include <ctime> #include <cstdlib> #define MAX 10000 using namespace std; int Max(int b[]) { int m[MAX],n=0,p=0; for(int i=0;i<4;i++) { for(int j=0;j<4;j++) { n=n+b[i+j]; m[p]=n; p++; } n=0; } int max=m[0]; for(int i=0;i<p;i++) { if(m[i]>max) max=m[i]; } return max; } int main() { int k[MAX],a[4][8],h[8]; int i; int j; cout<<"二维矩阵为:"<<endl; for(i=0;i<4;i++) { for(j=0;j<4;j++) { a[i][j]=rand()%100-50; a[i][j+4]=a[i][j]; cout<<a[i][j]<<" "; } cout<<endl; } for(i=0;i<4;i++) { k[i]=Max(a[i]); } int q=4; for(i=0;i<3;i++) { int t=0; for(j=0;j<8;j++) { h[t]=a[i][j]+a[i+1][j]; t++; } k[q]=Max(h); q++; } for(i=0;i<2;i++) { int t=0; for(j=0;j<8;j++) { h[t]=a[i][j]+a[i+1][j]+a[i+2][j]; t++; } k[q]=Max(h); q++; } int t=0; i=0; for(j=0;j<8;j++) { h[t]=a[i][j]+a[i+1][j]+a[i+2][j]+a[i+3][j]; t++; } k[q]=Max(h); q++; cout<<endl; int max=k[0]; for(i=0;i<q;i++) { if(k[i]>max) max=k[i]; } cout<<"最大子矩阵的值为:"; cout<<max<<endl; return 0; }
3.结果截图
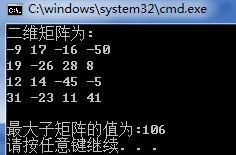
4.总结
思路尤为重要,这次练习在前边一维数组首尾相接的思路上,加以改善,就能够求得子数组的最大和。以前能够应用的一些算法或是函数也是很重要的。
5.结对
陈杰:思路以及程序编写
孟祥娟:测试以及博客发表