1.设计思想
要求得环形一维数组的最大子数组之和,首先要将其首尾相接。对于这个长度为n的一维数组,将其数组的前n-2项补在该一维数组的后面即可实现环形数组求最大子数组和。这样就形成了一个新数组,然后利用第一次求最大子数组和的算法,然后加上限定条件即子数组的长度不能超过整个数组的长度。但是也在该算法上进行了改动,先求出子数组的最小和,记录求得最小和时的子数组的起始和末尾下标。排除最小和之后的子数组则即为最大子数组的和。
2.源程序
#include <iostream> using namespace std; #include <cmath> #define N 1000 void main() { int n,i,a[N]; cout<<"请输入数组的个数:"; cin>>n; int m; m=2*n-2; cout<<"输入该数组:"<<endl; for(i=0;i<n;i++) { cin>>a[i]; } for(i=n;i<m;i++) { a[i]=a[i%n]; } cout<<"生成的新数组为:"<<endl; for(i=0;i<m;i++) { cout<<a[i]<<" ";; } int sum=0,b=0,x=0,y=0; int j=0; while((j-x)<n) { if(b>0) { b=a[j]; if(j<n) x=j; else break; } else { b+=a[j]; } if(sum>b) { sum=b; y=j; } j++; } cout<<endl; cout<<x<<endl<<y<<endl; int max_sum=0; for(i=y+1;i<m;i++) { max_sum+=a[i%n]; } cout<<"最大子数组和为:"<<max_sum<<endl; cout<<"数组分别为:"<<endl; for(i=y+1;i<m;i++) { cout<<a[i%n]<<" "; } cout<<endl; }
3.结果截图
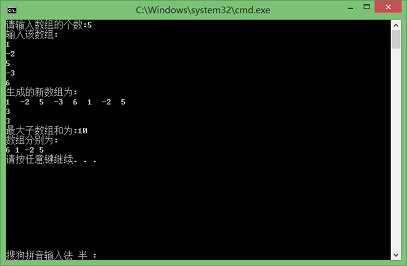
4.总结
在一开始想直接求最大子数组的和,但是经过测试之后发现有问题,就转到通过先求最小和再排除最小和包含的子数组以得到最大子数组和,通过这次练习,对思路的形成和完善有很大的影响。
5.结对成员
孟祥娟:思路以及程序的编写
陈杰:对程序的测试与审查