介绍
莫队算法是一个对于区间、树或其他结构离线(在线)维护的算法,此算法基于一些基本算法,例如暴力维护,树状数组,分块,最小曼哈顿距离生成树,对其进行揉合从而产生的一个简单易懂且短小好写的算法。此算法在很多情况下可以很轻松的切掉一些复杂而且难写的数据结构问题。
莫队的门槛
简单的说,莫队算法就是一个优美的暴力算法,假设操作数组的长度为n。在算法中,我们把数组分为sqrt(n)块,每一块的大小(长度)为sqrt(n)
MoDui_algorithm's thinking is to sort the inquiries offline and move several pointer to visit the wanted section
其他的介绍已经说的很详细了,这里就不画蛇添足了,
更多的信息在代码里,because program is the best language
莫队有一个众所皆知的入门题,想必很多人已经知道了。对!就是小Z的袜子
当我们完成一个询问时,只要将左右指针移动,并在每一次移动时更新当前的ans
这道题里我们需要将询问按照块来排序(若左指针在同一块,就按照右指针排序,否则就按照左指针排序)
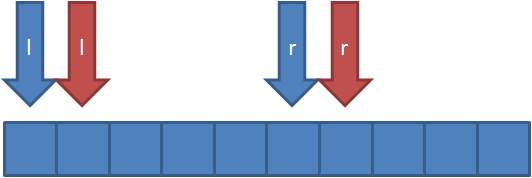
如上图所示,当我们已经求过蓝色指针范围内区间的ans,然后想要求红色指针范围内的ans,只要将左右指针向要求范围的方向移动即可
要注意的是在移动时我们必须更新ans,使其满足当前的区间
这是莫队的一个灵魂所在,没了这个操作莫队就失去了其魅力
手动模拟一下,你就会发现这种方式是多么的高效(每一个指针移动一次都只需要O(1)的时间)
像上图的那个情况,我们只要O(2)的时间,就可以求出下一个区间的信息
也许有的人会问如果没有排序会怎么样。。。如果没有排序,你可以自行脑补一下左右指针到处乱跳这般令人焦头烂额的场面,
O(n^2)的复杂度,还是洗洗睡了
莫队算法巧妙地将询问离线排序,使得其复杂度无比美妙……
这句话出自哪里我们暂且不论,但是这句话可以说是十分精辟的。这也正是莫队算法从暴力蜕变的第一步,也正是它的魅力所在
莫队的时间复杂度究竟到了怎样的一个令人发指的境界,我们也可以手动演算一下,最后求得的复杂度是O(n*sqrt(n))
当然,每一道题的复杂度都是不一样的,需要根据不同的情况来判断
至于解释就在代码里面了
注意:一定要先看题目再看代码,否则你可能会一脸懵逼
#include<cstdio> #include<algorithm> #include<cmath> #define f(b) for(int i=1;i<=b;i++) #define ll long long using namespace std;const int N=50003; struct Mo{int l,r,ID;ll A,B;}q[N];//build a Mo_Dui struct //l:left point r:right point ID:read_order ll S(ll x){return x*x;} ll GCD(ll a,ll b){while(b^=a^=b^=a%=b);return a;} //work out greatest_common_divisor of two numbers int n,m,col[N],unit,Be[N];ll sum[N],ans; //sum is used to mark each color's sum //ans is used to mark present_block's information //col is used to mark each position's color //Be is to mark each color's block bool cmp(Mo a,Mo b){return Be[a.l]==Be[b.l]?a.r<b.r:a.l<b.l;} //if their left pointer are in the same block(part),just compare their right pointer to put them in order //or,just compare their left pointer to put them in order bool CMP(Mo a,Mo b){return a.ID<b.ID;}; //this compare function's work is to sort the array depends on read_order void revise(int x,int add){ans=ans-S(sum[col[x]])+S(sum[col[x]]+=add);} int main(){ //here ,we divide the array into sqrt(n) blocks(parts),and each block(part)'s size is sqrt(n) //if you don't know ,you can return to primary school and have a study(primary school's Olympic Mathematics) scanf("%d%d",&n,&m);//read the total_num of socks and the total_num of inquiries unit=sqrt(n);//mark down sqrt(n) f(n)//make a loop from 1 to n in order to read each sock's color scanf("%d",&col[i]),Be[i]=i/unit+1;//read the color and mark it's block(part) f(m)scanf("%d%d",&q[i].l,&q[i].r),q[i].ID=i;//read the chosen section and mark its read_order sort(q+1,q+m+1,cmp);//sort the inquiries to make them in order(in this way,we can move pointer more easier) //one of Mo_Dui_algorithm's features:offline sort optimization int l=1,r=0;//initializate left_pointer as 1 and right_pointer as 0 f(m)//make a loop from 1 to m in order to visit each inquiry {while(l<q[i].l)revise(l,-1),l++;//if the left_pointer is smaller than the wanted_left_pointer,just renew the answer and move the left_pointer while(l>q[i].l)revise(l-1,1),l--;//if the left_pointer is bigger than the wanted_left_pointer,just renew the answer and move the left_pointer while(r<q[i].r)revise(r+1,1),r++;//if the right_pointer is smaller than the wanted_right_pointer,just renew the answer and move the right_pointer while(r>q[i].r)revise(r,-1),r--;//if the right_pointer is bigger than the wanted_right_pointer,just renew the answer and move the right_pointer if(q[i].l==q[i].r){q[i].A=0;q[i].B=1;continue;}//if the two points are the same,just mark the answer(no solution)and jump to next inquiry //or,just means it may has solution q[i].A=ans-(q[i].r-q[i].l+1);//work out the probability_fraction's numerator q[i].B=1LL*(q[i].r-q[i].l+1)*(q[i].r-q[i].l);//work out the probability_fraction's denominator ll gcd=GCD(q[i].A,q[i].B);q[i].A/=gcd;q[i].B/=gcd;//change the fraction into fraction in lowest terms }sort(q+1,q+m+1,CMP);//sort the inquiries in order to put them in read_order f(m)printf("%lld/%lld ",q[i].A,q[i].B);return 0;}//out the answer
什么?还是不懂?那就对照着代码看接下来的讲解吧
如图,当前完成的询问的区间为[a,b],下一个询问的区间为[p,q],现在保存[a,b]区间内的每个颜色出现次数的sum[]数组已经准备好,[a,b]区间询问的答案Ans1已经准备好,怎样用这些条件求出[p,q]区间询问的Ans2?

考虑指针向左或向右移动一个单位,我们要付出多大的代价才能维护sum[]和Ans(即使得sum[],Ans保存的是当前[l,r]的正确信息)。我们对图中l,r的向右移动一格进行分析:
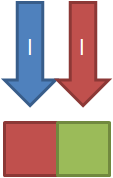
如图,l指针向右移动一个单位,所造成的后果就是:我们损失了一个红色方块。那么怎样维护?美妙地,sum[红色]减去1。那Ans如何维护?先看分母,分母从n2变成(n-1)2,分子中的其他颜色对应的部分是不会变的,红色却从sum[红色]2变成(sum[红色]-1)2 ,为了方便计算我们可以直接向给Ans减去以前该颜色的答案贡献(即sum[红色]2)再加上现在的答案贡献(即(sum[红色]-1)2 )。同理,观赏下面的r指针移动,将是差不多的。
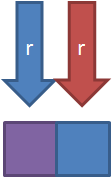
·如图r指针的移动带来的后果是,我们多了一个蓝色方块。所以操作和上文相似,只不过是sum[蓝色]++。
进阶1:带修莫队(可持久化莫队)
话说我第一次接触的关于莫队的题目就是带修莫队
上面的那句话手动无视掉,开始接下来的讲解,带修莫队,可以说在计算机题目中也算比较常见的
所以学习它是非常必要的。
带修莫队是什么?字面上的意思,就是带修改操作的莫队算法。
和上面一样,我先放出例题:数颜色
和上面的小Z的袜子一样,这道题也是一道众所皆知的莫队题目,因为题目的要求十分直观,就用它作为带修莫队的入门题
这道题我们需要用到一个新的指针:时间指针,用来记录当前询问是在第几次修改之后的
放出代码,对照题目欣赏美妙的实现过程
#include<cstdio> #include<algorithm> #include<cmath> #define f(b) for(int i=1;i<=b;i++) using namespace std;const int N=10003; struct Query{int l,r,Tim,ID;}q[N]; //l: inquiry_section's left_border r: inquiry_section's right_border //Tim :this inquiry's change_times ID:inquiry_order struct Change{int pos,New,Old;}c[N];//the highlight part 1!! persistent-marked array //pos: the position changed //New: this position's new color //Old: this position's previous color int n,m,s[N],color[N*100],Time,t,now[N],unit,Be[N],ans[N],Ans,l=1,r,T; //s[]:each colorpen's present_color depends on read_order //Be[]:mark each location's block //now[]:mark each location's present color //unit:the size(length) of each block //ans[]:against each inquiry,mark it's answer //l: present left_pointer r:present right_pointer Ans:present answer T:present time //n:total_number of colorpens m:total_number of inquiries t,Time:iterator //color:marked each color's number bool cmp(Query a,Query b){return Be[a.l]==Be[b.l]?(Be[a.r]==Be[b.r]?a.Tim<b.Tim:a.r<b.r):a.l<b.l;} //if their left_pointers are in the same block just compare their right_pointers' block, // if their right_pointers are in the same block ,just sort them depends on change_times, // or just sort depends on their right_pointer //if their left_pointers are not in the same block,just sort depends on their left_pointers void revise(int x,int d){color[x]+=d;if(d>0)Ans+=color[x]==1;if(d<0)Ans-=color[x]==0;}//the highlight part 2!! revise_operation //change this color's number ,if have add this color's num:if color[x]!=1,just means it has been add into the Ans or just means has not and add it into the Ans //if have minus this color's num: if color[x]!=0,just means this color is still real inside the present_inquiry_section.Or ,just means this color isn't real inside the present_inquiry_section,just renew the Ans void going(int x,int d){if(l<=x&&x<=r)revise(d,1),revise(s[x],-1);s[x]=d;} //if x is inside the section ,just operate on it:add the new color and minus the previous color //at last change the colorpen's color int main(){scanf("%d%d",&n,&m);//read the total_number of colorpens and the total_number of inquiries unit=pow(n,0.666666);//set the size of each block f(n)scanf("%d",&s[i]),now[i]=s[i],Be[i]=i/unit+1;//make a loop from 1 to n in order to read each colorpen's color //mark this location's color,and its block f(m){char sign;int x,y;scanf(" %c %d%d",&sign,&x,&y);//read the kind of inquiry,x,and y if(sign=='Q')q[++t]=(Query){x,y,Time,t};//if the kind is Q,just means it asked for different_colorpens_num between x and y //just push it into the query_array else c[++Time]=(Change){x,y,now[x]},now[x]=y;//or ,just the kind is R,it wanted to revise x's color into y //just pish it into the change_array,and change this location's color } sort(q+1,q+t+1,cmp);//sort the query_array depends on incremental order f(t){//make a loop from 1 to t in order to deal with each inquiry while(T<q[i].Tim)going(c[T+1].pos,c[T+1].New),T++; //if the now_time is smaller than the wanted time ,just change the color into the present_time's color and renew the time while(T>q[i].Tim)going(c[T].pos,c[T].Old),T--; //if the now_time is larger than the wanted time , just change the color into the previous_time's color and renew the time while(l<q[i].l)revise(s[l],-1),l++; //if the present left_pointer is smaller than the wanted left_pointer ,just move the left_pointer to right,renew the Ans and the present_color_number while(l>q[i].l)revise(s[l-1],1),l--; //if the present left_pointer is larger than the wanted left_pointer ,just move the left_pointer to left ,renew the Ans and the present_color_number while(r<q[i].r)revise(s[r+1],1),r++; //if the present right_pointer is smaller than the wanted right_pointer ,just move the right_pointer to right ,renew the Ans and the present_color_number while(r>q[i].r)revise(s[r],-1),r--; //if the present right_pointer is larger than the wanted right_pointer ,just move the right_pointer to left ,renew the Ans and the present_color_number ans[q[i].ID]=Ans;//mark the answer depends on inquiry_order }f(t)printf("%d ",ans[i]);return 0;}//out the answer
时间复杂度为O(unit*n+n2/unit+(n/unit)2*n),还是很可观的QAQ
至于过程,本质性的和普通莫队差不多,至于详细过程,就观摩上面的程序吧
进阶2:树上带修莫队
虽然觉得有了上面的讲解,树上带修莫队也不算问题,但因为这一类题目比较典型,还是仁慈地讲一讲
无视上面的那句话,进入本篇博文目前的最终章——树上带修莫队
树上带修莫队是什么?字面上的意思,在一棵树上进行带修莫队
实现的过程和带修莫队并没有什么区别
好吧,还是有一些区别的,首先是分块的问题,很多人可能会问,那么大一坨树,该怎么对它进行分块呢?
这一点初学者一脸懵逼也是很正常的,毕竟树上莫队不比普通莫队那么直观,只要在一条线上胡乱分块即可
而树有分支,每一棵子树的情况也不尽相同。很多人听到这个名字就会感到五雷轰顶之感。
但是,我在这里负责任地告诉你,树上带修莫队也同样简单
依旧是熟悉的配方,按题目情况分unit
分块的目的是为了快速访问与查找
这句话是一位巨神说的。确实这样,学习一个算法的过程,就是由浅入深,由深入浅的过程。
学了这么多,我们又回到了算法的本质,也正是该算法的灵魂。分块是为了什么?就是为了快速访问和查找啊!
同样的步骤,将一棵树分成若干块,每一块的大小<=unit
尝试在树上构造相邻的块,使得:块内元素的互相访问的移动次数控制在一个范围内(也就是unit)。做法是用栈维护当前节点作为父节点访问它的子节点,当从栈顶到父节点的距离大于unit时,弹出这部分元素分为一块。
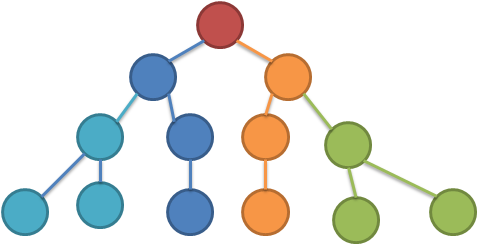
如图,相同颜色的分为一块。另外,对于剩余分块的节点,也就是根节点附近由于个数小于unit而形成的一坨点,最后再分一块或加在最后一块中
在该图中根节点为剩余分块的节点,它单独分一块
这样分有什么好处呢?这样分可以使每一个块内的点到达另一个点最多移动unit次(具体看普通莫队)
解决了分块的问题,另外一个问题也接踵而至——树上指针移动问题。
又是给新学者的一个沉重打击,但是方法也同样简单,树是弯的怎么办?把弯的掰直啊!
试想一下,从现指针到目标指针的路径,本质上就是一条线,线上的指针移动,其实跟普通莫队差不多,只不过需要遵循一些树的规则罢了
多说无益,入门题奉上:Haruna’s Breakfast
在访问时,我们用vis[u]来记录u是否被访问过
如何进行维护呢?常见的维护方法是离散化加数据结构。其实也没有什么定性要求,用分块,树状数组还是其它的玄学数据结构全凭个人的喜好
先放出代码一睹为快吧
void ADD(int from,int to){e[k]=(E){to,head[from]};head[from]=k++;} void dfs(int u){fr(i,1,19)if((1<<i)>deep[u])break;else fa[u][i]=fa[fa[u][i-1]][i-1]; int bottom=top; tf(i,head,u)if(to!=fa[u][0]){fa[to][0]=u;deep[to]=deep[u]+1;dfs(to); if(top-bottom>=unit){m++;while(top!=bottom)Be[st[top--]]=m;}}st[++top]=u;} int LCA(int x,int y){if(deep[x]<deep[y])swap(x,y);int Dis=deep[x]-deep[y]; fr(i,0,16)if((1<<i)&Dis)x=fa[x][i];if(x==y)return x; fd(i,16,0)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];return x==y?x:fa[x][0];} struct Change{int u,New,Old;}cq[N]; struct Query{int u,v,tim,id; bool operator <(const Query &a) const{return Be[u]==Be[a.u]?(Be[v]==Be[a.v]?tim<a.tim:Be[v]<Be[a.v]):Be[u]<Be[a.u];}}q[N]; struct Datalock{struct _blo{int l,r;}b[350]; int n,Be[N],m,unit,num[N],sum[350]; void init(){unit=sqrt(n);m=(n-1)/unit+1;fr(i,1,n)Be[i]=(i-1)/unit+1; fr(i,1,m)b[i].l=(i-1)*unit+1,b[i].r=i*unit;b[m].r=n;} void Add(int v){if(v<=n)sum[Be[v]]+=(++num[v])==1;} void Del(int v){if(v<=n)sum[Be[v]]-=(--num[v])==0;} int mex(){fr(i,1,m)if(sum[i]!=b[i].r-b[i].l+1) fr(j,b[i].l,b[i].r)if(!num[j])return j;return -1;}}Data; void revise(int u,int d){if(vis[u])Data.Del(a[u]),Data.Add(d);a[u]=d;} void Run(int u){if(vis[u])Data.Del(a[u]),vis[u]=0;else Data.Add(a[u]),vis[u]=1;} void move(int x,int y){ if(deep[x]<deep[y])swap(x,y); while(deep[x]>deep[y])Run(x),x=fa[x][0];while(x!=y)Run(x),Run(y),x=fa[x][0],y=fa[y][0];} void Mo(){fr(i,1,p){ while(T<q[i].tim)T++,revise(cq[T].u,cq[T].New); while(T>q[i].tim)revise(cq[T].u,cq[T].Old),T--; if(u!=q[i].u)move(u,q[i].u),u=q[i].u;if(v!=q[i].v)move(v,q[i].v),v=q[i].v; int anc=LCA(u,v);Run(anc);ans[q[i].id]=Data.mex()-1;Run(anc);}}
其中有很多部分都是和带修莫队差不多
你看到了什么,LCA???,对的,这也是树上莫队和普通莫队的区别,除了访问数组,还要处理到达公共祖先的特殊情况
为什么会有特殊情况?让我来手动模拟一遍来解释它
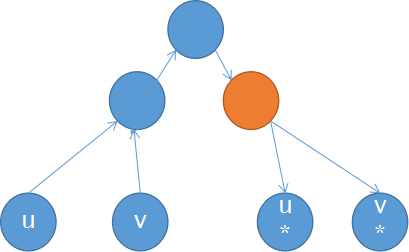
如图所示情况
u,v两个指针在经过根节点之前都没有发生什么怪异情况,
但是当它们经过u*,v*(即当前查询的区间两指针)的最近公共祖先节点(橙色强调出来的惨案现场)时
void Run(int u){if(vis[u])Data.Del(a[u]),vis[u]=0;else Data.Add(a[u]),vis[u]=1;}
显而易见,它被标注了两次,这意味着它被设为没访问过
没有加上LCA的程序的BUG正是在此,而这显然不是我们想要看到的
这就是LCA的用处了,它打破了重复标注的怪圈,使程序重新变得和平
除此之外还要强调一点,上面所说的维护的数据结构没有维护LCA点的信息
每次u,v归位后,我们单独为LCA计算一次,这样既避免了怪异情况影响答案,有保证了LCA对答案的贡献。
接下来是详细代码。接下来的一幕可能会伤害到你幼小的心灵,
但我已经竭尽所能码的最明了了QAQ。。。。。。
#include<cstdio> #include<algorithm> #include<cmath> #define ct register int #define ff(b) for(ct i=1;i<=b;i++) #define fr(i,a,b) for(ct i=a;i<=b;i++) #define fd(i,a,b) for(ct i=a;i>=b;i--) #define tf(i,a,x) for(ct i=a[x],to=e[i].to;i;i=e[i].next,to=e[i].to) int in(){ct x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while('0'<=ch&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}return x*f;} using namespace std; /*--global variables--*/ const int N=50009; int unit,Be[N],m,ans[N],vis[N]; //unit:the size(length) of each block //Be[]:mark each location's block //m:total_number of inquiries //ans[]:against each inquiry,mark it's answer //vis[]:mark each endpoint if it has been visited int st[N],top;//stack int fa[N][18],deep[N]; //fa[][]:each endpoint's father //deep: each endpoint's deep int a[N],u=1,v=1,T; //T,u,v:iterator //a[]:each point's delicious_num int tim,p;//counters /*--global variables above--*/ /*--edge--*/ int cnt=1,head[N]; struct E{int to,next;}e[N*3];//edge //v:to_endpoint next:from_endpointer's point void ADD(int from,int to){e[cnt]=(E){to,head[from]};head[from]=cnt++;}//add edge /*--edge above--*/ /*--Mo struct--*/ struct Change{int u,New,Old;}cq[N];//persistent-marked array //pos: the position changed //New: this position's new color //Old: this position's previous color struct Query{int u,v,tim,id; //u: inquiry_section's left_border v: inquiry_section's right_border //Tim :this inquiry's change_times id:inquiry_order bool operator <(const Query &a) const{return Be[u]==Be[a.u]?(Be[v]==Be[a.v]?tim<a.tim:Be[v]<Be[a.v]):Be[u]<Be[a.u];}}q[N]; //encapsulate the block_struct,set compare_function inside /*--Mo struct above--*/ //--------- struct Datalock{ struct _blo{int l,r;}b[350];//pointer //l: present left_pointer r:present right_pointer int n,Be[N],m,unit,num[N],sum[350]; //n:total_number of colorpens //Be[]:mark each location's block //m:total_number of inquiries t,Time:iterator //unit:the size(length) of each block //num:marked each color's number void init(){unit=sqrt(n);m=(n-1)/unit+1;ff(n)Be[i]=(i-1)/unit+1; ff(m)b[i].l=(i-1)*unit+1,b[i].r=i*unit;b[m].r=n;} void Add(int v){if(v<=n)sum[Be[v]]+=(++num[v])==1;} void Del(int v){if(v<=n)sum[Be[v]]-=(--num[v])==0;} int mex(){ff(m)if(sum[i]!=b[i].r-b[i].l+1) fr(j,b[i].l,b[i].r)if(!num[j])return j;return -1;}}Data; //----------encapsulate the revise_operation void dfs(int u){ff(19)if((1<<i)>deep[u])break;else fa[u][i]=fa[fa[u][i-1]][i-1]; int bottom=top; tf(i,head,u)if(to!=fa[u][0]){fa[to][0]=u;deep[to]=deep[u]+1;dfs(to); if(top-bottom>=unit){m++;while(top!=bottom)Be[st[top--]]=m;}}st[++top]=u;} int LCA(int x,int y){if(deep[x]<deep[y])swap(x,y);int Dis=deep[x]-deep[y]; fr(i,0,16)if((1<<i)&Dis)x=fa[x][i];if(x==y)return x; fd(i,16,0)if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];return x==y?x:fa[x][0];} void revise(int u,int d){if(vis[u])Data.Del(a[u]),Data.Add(d);a[u]=d;} //revise_operation:delt the old_num's message and add the new_num's message,at last change the num void Run(int u){if(vis[u])Data.Del(a[u]),vis[u]=0;else Data.Add(a[u]),vis[u]=1;} //visit operation:if u has been visited,just delt its message,and mark it has not been visited //or,just add its message and mark it has been visited void move(int x,int y){if(deep[x]<deep[y])swap(x,y); while(deep[x]>deep[y])Run(x),x=fa[x][0];while(x!=y)Run(x),Run(y),x=fa[x][0],y=fa[y][0];} //move operation:move from the deeper one to another one ,until they are in the same deep //then there are two cases: //case 1:they are same,just means has moved from x to y,just return //case 2:they are different,just means they are in the different side of their LCA,just move them bove,until they meet int main(){int uu,vv,op,x,y,n,Q,t[N]; scanf("%d%d",&n,&Q);//read the total_number of points and the total_number of operations unit=pow(n,0.45);//work out the unit ff(n)a[i]=in(),t[i]=++a[i];//read each point's delicious_num ff(n-1)uu=in(),vv=in(),ADD(uu,vv),ADD(vv,uu);//read each edge,add this edge dfs(1);//initialization while(top)Be[st[top--]]=m;//if some points don't have its block,just set them together as the last block ff(Q){op=in(),x=in(),y=in();//read the operation and two num if(op)p++,q[p]=(Query){x,y,tim,p};//query_operation,just want present smallest absent_natural_number //just push it into to query_array else tim++,cq[tim]=(Change){x,y+1,t[x]},t[x]=y+1;//revise_operation,just push it into the change_array and change it }Data.n=n+1;Data.init();//initialization sort(q+1,q+1+p);//sort the query_array depends on incremental order ff(p){//make a loop from 1 to p in order to deal with each inquiry while(T<q[i].tim)T++,revise(cq[T].u,cq[T].New); //if the now_time is smaller than the wanted time ,just change the num into the present_time's num and renew the time while(T>q[i].tim)revise(cq[T].u,cq[T].Old),T--; //if the now_time is larger than the wanted time , just change the color into the previous_time's color and renew the time if(u!=q[i].u)move(u,q[i].u),u=q[i].u;if(v!=q[i].v)move(v,q[i].v),v=q[i].v; //if the now_left_pointer and now_left_pointer are not in the wanted position,just move them int anc=LCA(u,v);Run(anc);ans[q[i].id]=Data.mex()-1;Run(anc); //extra operation:calculate out the LCA's message }ff(p)printf("%d ",ans[i]);//out the answer }
对于三个常见莫队题型已经讲解完毕,之后可能会补上一些莫队题目,总之,未完待续