软件工程第二次作业

博客信息	沈阳航空航天大学计算机学院2020软件工程作业
作业要求	https://edu.cnblogs.com/campus/sau/Computer1701-1705/homework/10583
课程目标	熟悉一个“高质量”软件的开发过程
作业目标	单元测试练习

一、题目要求

问题：给定n个整数（可能为负数）组成的序列a[1], a[2], a[3], …, a[n], 求该序列如a[i] + a[i + 1] + … + a[j]的子段和的最大值。
当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为：Max{ 0,a[i] + a[i + 1] + … + a[j] }, 1 <= i <= j <= n。
例如：当（a[1], a[2], a[3], a[4], a[5], a[6]） = (-2, 11, -4, 13, -5, -2)时，最大子段和为20。

解决方法

1. 暴力解法
   sum[i..j]为数组中第i个元素到第j个元素的和（其中0<=i<j<=n-1），通过遍历所有的组合之和，就能找到最大的一个和了

#include "stdafx.h"
//暴力法求最大子数组和问题
int _tmain(int argc, _TCHAR* argv[])
{
    int A[8] = { -6, 10, -5, -3, -7, -1, -1 };
    int array_length = sizeof(A) / sizeof(A[0]);//数组大小
    int sum = -10000;//记录子数组的和
    int low;//记录子数组的底
    int height;//记录子数组的高
    for (int i = 0; i < array_length; i++)
    {
        for (int j = i ; j < array_length; j++)
         {
            int subarraysum=0;//所遍历出来的子数组的和
            //计算遍历的子数组之和
            for (int k = i; k <= j; k++)
            {
               subarraysum += A[k];
             }
             //找出最大的子数组
            if (subarraysum>sum)
             {
                sum = subarraysum;
                low = i;
                height = j;
             }
        }   
}
printf("%d  %d  %d", low, height,sum);//将结果打印出来
getchar();
return 0;
}

显而易见，此程序的时间复杂度为O（n3），所以不推荐这种。

2.分治法
我们把数组A[1..n]分成两个相等大小的块：A[1..n/2]和A[n/2+1..n]，最大的子数组只可能出现在三种情况：
A[1..n]的最大子数组和A[1..n/2]最大子数组相同；
A[1..n]的最大子数组和A[n/2+1..n]最大子数组相同；
A[1..n]的最大子数组跨过A[1..n/2]和A[n/2+1..n]
前两种情况的求法和整体的求法是一样的，因此递归求得。
第三种，我们可以采取的方法也比较简单，沿着第n/2向左搜索，直到左边界，找到最大的和maxleft，以及沿着第n/2+1向右搜索找到最大和maxright，那么总的最大和就是maxleft+maxright。
而数组A的最大子数组和就是这三种情况中最大的一个。
伪代码如下：

  #include "stdafx.h"
   //分治法求最大子数组和问题
  struct PositioASum {
     int low;
     int high;
     int sum;
  };
  //寻找包含中点位置的最大子数组函数
  PositioASum MaxCrossingSubarray(int a[], int low, int mid, int high)
  {
    //求中点左边的最大值和最大位置
    int maxLeft;//记录左边的最大位置
    int maxSumLeft=-10000;//记录左边的最大和
    int sumLeft=0;
    for (int i = mid; i >= low; i--)
     {
       sumLeft += a[i];
       if (sumLeft > maxSumLeft)
        {
          maxSumLeft = sumLeft;
          maxLeft = i;
        }
     }
    //求中点右边的最大值和最大位置
    int maxRight=mid+1;//记录右边的最大位置
    int maxSumRight = -10000;//记录右边的最大和
    int sumRight = 0;//记录右边子数列的和
    for (int i = mid+1; i <= high; i++)
      {
       sumRight += a[i];
       if (sumRight > maxSumRight)
        {
         maxSumRight = sumRight;
         maxRight = i;
       }
    }
    PositioASum ps;
    ps.low = maxLeft;
    ps.high = maxRight;
    ps.sum = maxSumLeft + maxSumRight;
       return ps;
 }
 //分治法
 PositioASum FindMaxSubArray(int a[], int low, int high)
 {
     if (low == high)
      {
        PositioASum ps;
        ps.low = low;
        ps.high = high;
        ps.sum = a[low];
         return ps;
      }
    else{
         int mid = (low + high) / 2;
         PositioASum left = FindMaxSubArray(a, low, mid);
         PositioASum right = FindMaxSubArray(a, mid + 1, high);
         PositioASum cross = MaxCrossingSubarray(a, low, mid, high);
         if (left.sum >= cross.sum && left.sum >= right.sum)
         {
            return left;
          }
         else if (right.sum >= left.sum && right.sum >= cross.sum)
             {
               return right;
             }
              else{
                   return cross;
                }
         }
  }
 
 int _tmain(int argc, _TCHAR* argv[])
  {
      int A[8] = {-1,0,0,0,-1};
      PositioASum result = FindMaxSubArray(A, 0, 4);
      printf("%d  %d  %d", result.low, result.high, result.sum);//将结果打印出来
       getchar();
       return 0;
}

算法的时间复杂度为O（nlogn）,由于本程序是在数组的原地址上面进行的，所以总体的控件复杂度为递归的时间复杂度+数组所占的空间为S（n）+S（logn）=S(n)

3.动态规划
令cursum(i)表示数组下标以i为起点的最大连续下标最大的和，而maxsum(i)表示前i个元素的最大子数组之和。那么我们就可以推出下一个maxsum(i+1)应该为cursum(i+1)和maxsum(i)中选取一个最大值。递推式为：
cursum(i) = max{A[i],cursum(i-1)+A[i]};
maxsum(i) = max{maxsum(i-1),cursum(i+1)};
代码如下：

 //在线法求最大子数组和问题
int _tmain(int argc, _TCHAR* argv[])
 {
   int A[8] = { -6, 10, -5, 6, -7, -1, -1 };
   int array_length = sizeof(A) / sizeof(A[0]);//数组大小
   int sum = 0;//记录子数组的和
   int thisSum = 0;
   int low=0;//记录子数组的底
   int height=0;//记录子数组的高
   for (int i = 0; i < array_length; i++)
   {
      thisSum += A[i];
      if (thisSum > sum)
       {
         sum = thisSum;
       }
      else if (thisSum < 0)
       {
        thisSum = 0;
       }
  }
   printf("%d",sum);//将结果打印出来
   getchar();
   return 0; 
}

这种算法时间复杂度只是O(n)，效果非常好！

二、代码链接

有点意思

三、运行结果

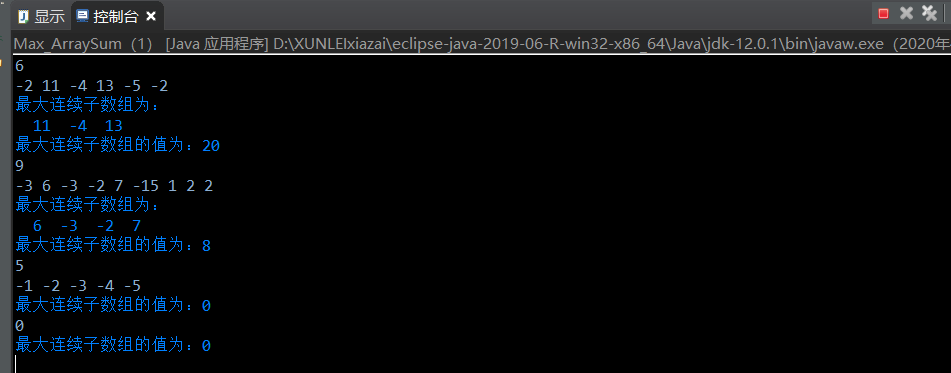
四、流程图设计

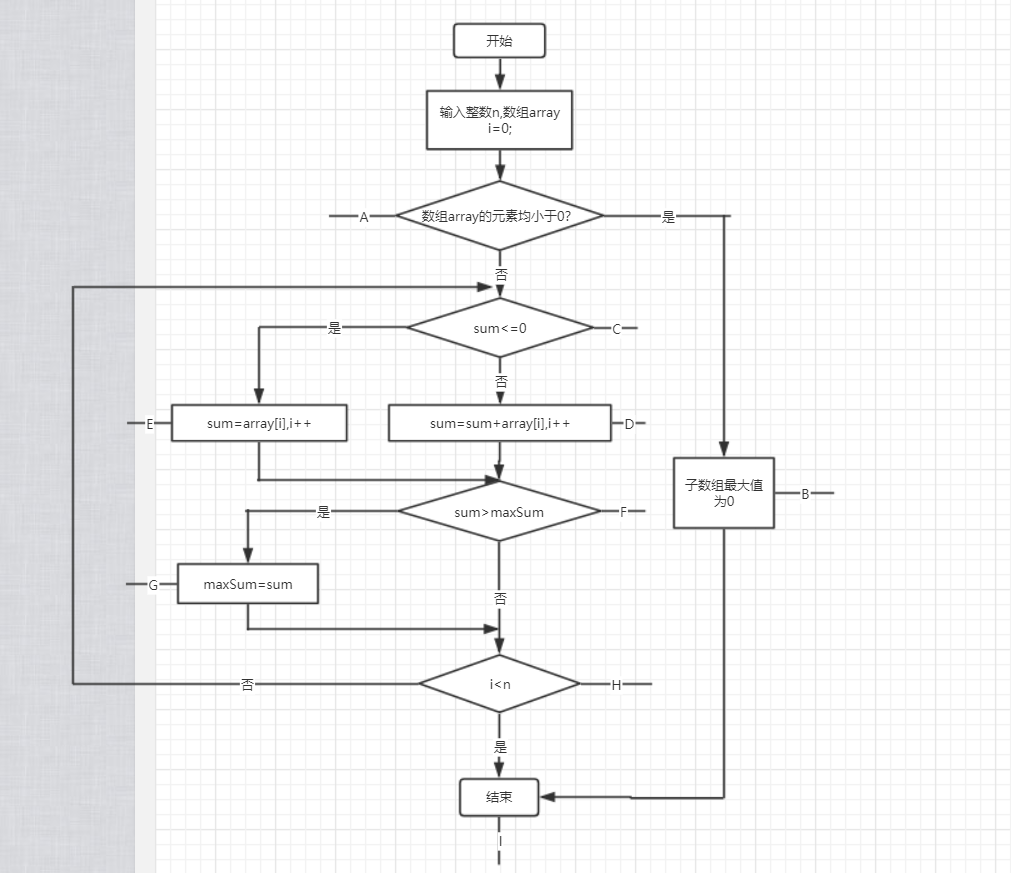
条件组合	执行路径
array>0	ABI
array<0,sum<=0,sum>maxSum	ACEFGHI
array<0,sum>0,sum>maxSum	ADFGHI
array<0,sum>0,sum<=maxSum	ACDFHI
array<0,sum<=0,sum<=maxsum	ACEFHI

实例（2,2,-4,2）的执行路径可覆盖：ACEFGHI、ADFGHI、ACDFHI、ACEFHI
实例（-1,-2,-3,-4,-5）的执行路径可覆盖：ABI

五、单元测试工具

编译环境为Eclipse里自带工具JUnit4单元测试工具

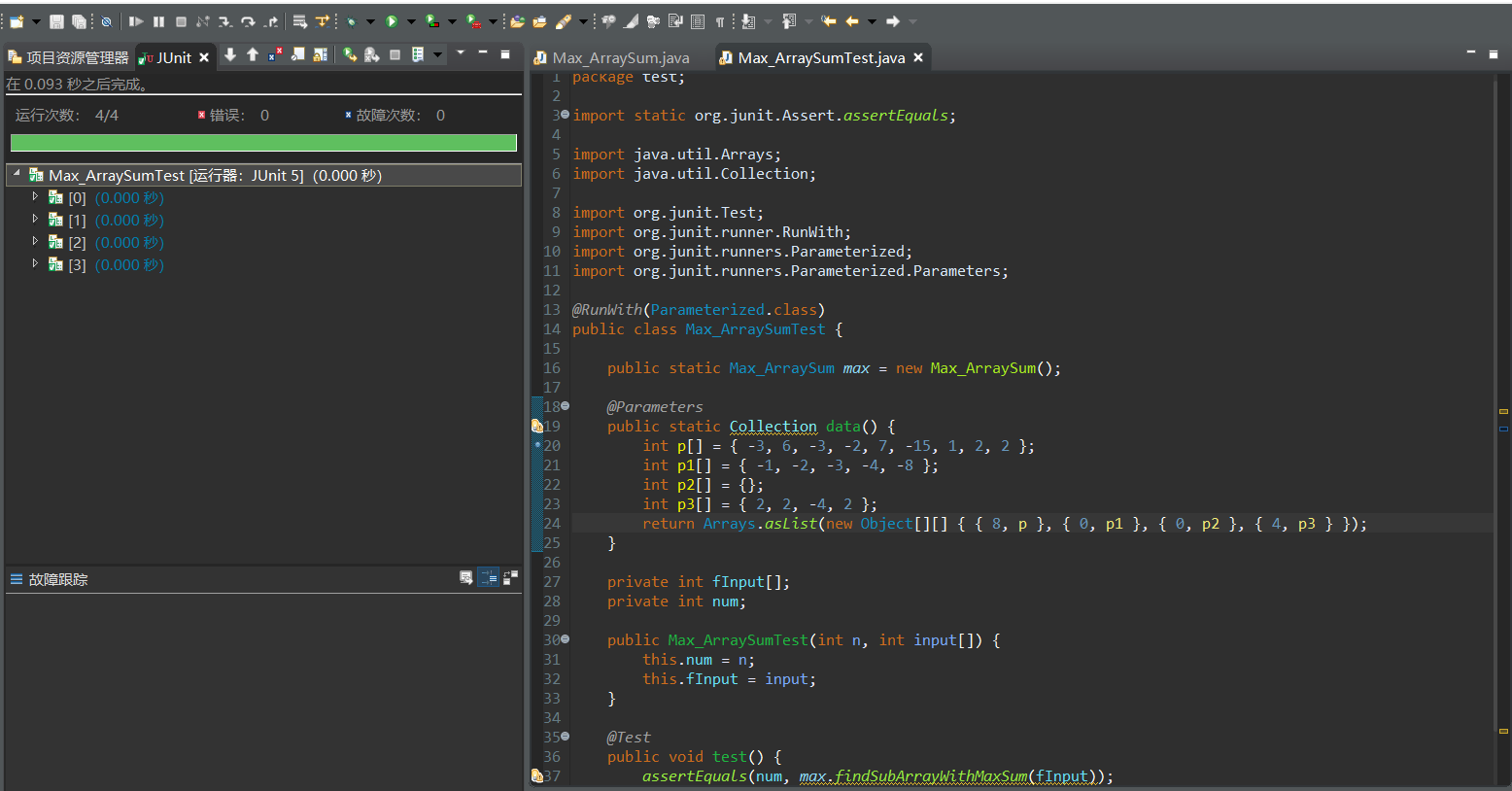
六、工作日志

项目	记录结果
日期	2020年4月3日
开始时间	01：30
结束时间	24:30
编码行数	97
错误数量	2
错误1	当输入n=0时，计算结果不为0
错误1修改时间	2 min
错误2	JUnit4 中的参数化自动测试运行报错
错误2修改时间	1.5 h

七、体会

这次作业是让我们熟悉“高质量”软件开发过程，虽让我们这次只是做一个程序的开发，但我也从中学到了很多。
比如：针对你的程序的流程图如何去设计测试用例，使用例尽可能的覆盖到各个语句判断、分支等等，不止走的通的路能走，走不通的路也得设计能走通。
还学会了Eclipse中的单元测试工具和参数化自动测试的方法。感觉自己还是欠缺许多，还得继续努力。