机器学习--分类问题
分类问题是监督学习的一个核心问题,它从数据中学习一个分类决策函数或分类模 型(分类器(classifier)),对新的输入进行输出预测,输出变量取有限个离散值。

决策树
决策树(decision tree)是一个树结构,每个非叶节点表示一个特征属性,每个分支
边代表这个特征属性在某个值域上的输出,每个叶节点存放一个类别。
决策过程:从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,
直到到达叶子节点,将叶子节点存放的类别作为决策结果。
给定训练数据,如何构建决策树呢?
1. 特征选择:选取对训练数据具有分类能力的特征。
2. 决策树生成:在决策树各个点上按照一定方法选择特征,递归构建决策树。
3. 决策树剪枝:在已生成的树上减掉一些子树或者叶节点,从而简化分类树模型。
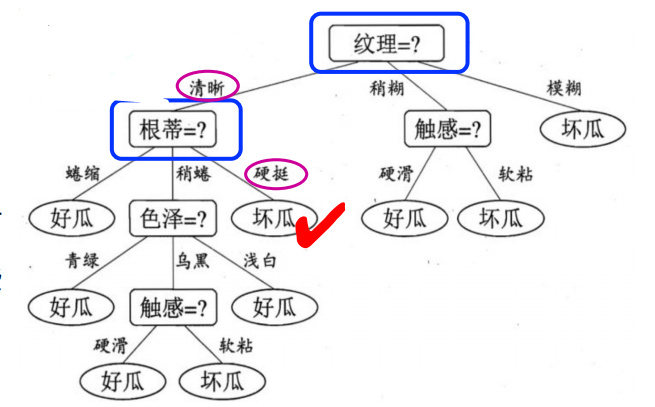
示例:假如我买了一个西瓜,它的特点是纹理清晰、根
蒂硬挺,如何根据右侧决策树判断是好瓜还是坏瓜?
核心算法
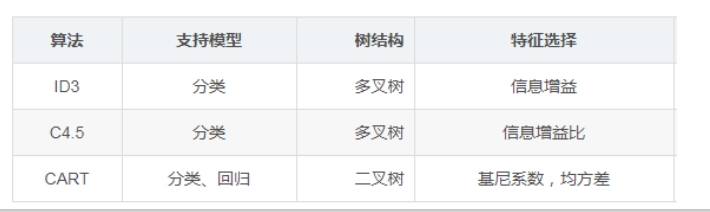
ID3算法,C4.5算法及CART算法
决策树特征选择
决策树构建过程中的特征选择是非常重要的一步。特征选择是决定用哪个特征来划分 特征空间,特征选择是要选出对训练数据集具有分类能力的特征,这样可以提高决策树的 学习效率。
信息熵:表示随机变量的不确定性,熵越大不确定性越大。
信息增益:信息增益 = 信息熵(前) - 信息熵(后)
信息增益比: 信息增益比 = 惩罚参数 * 信息增益。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。
基尼指数:表示集合的不确定性,基尼系数越大,表示不平等程度越高。

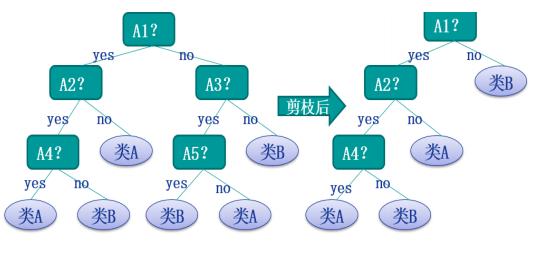
在生成树的过程中,如果没有剪枝(pruning)操作,就会生成一个队训练集完全 拟合的决策树,但这是对测试集非常不友好的,泛化能力不行。因此,需要减掉一些枝 叶,使得模型泛化能力更强。
理想的决策树有三种:叶子节点数最少、 叶子节点深度最小、叶子节点数最少且 叶子节点深度最小。
预剪枝 通过提前停止树的构建而对树剪枝,一旦停止,节 点就是叶子,该叶子持有子集中最频繁的类。 定义一个高度,当决策树达到该高度时就停止生长 达到某个节点的实例具有相同的特征向量 定义一个阈值(实例个数、系统性能增益等) 后剪枝方法 首先构造完整的决策树,然后对那些置信不够的结点子树用叶子结点来代替,该叶子的类 标号用该结点子树中最频繁的类标记。相比于预 剪枝,这种方法更常用,因为在预剪枝方法中精 确地估计何时停止树增长很困难。
贝叶斯分类
贝叶斯分类是基于贝叶斯定理和属性特征条件独立性的分类方法。 贝叶斯流派的核心:Probability theory is nothing but common sense reduced to calculation. 概率论只不过是把常识用数学公式表达了出来。——拉普拉斯
案例:假设春季感冒流行,你同桌打了一个喷嚏,那你
同桌感冒了的概率是多少?
1. 计算先验概率:你同桌没有任何症状的情况下可能得感冒 的概率是多少?
2. 为每个属性计算条件概率:如果你同桌感冒了, 那么 他会打喷嚏的概率是多少, 如果他没感冒, 出现打喷嚏症状的概 率有多少?
3. 计算后验概率:根据1 和2求解最终问题,这才是拥有贝 叶斯思想的你该做的分析。
贝叶斯理论 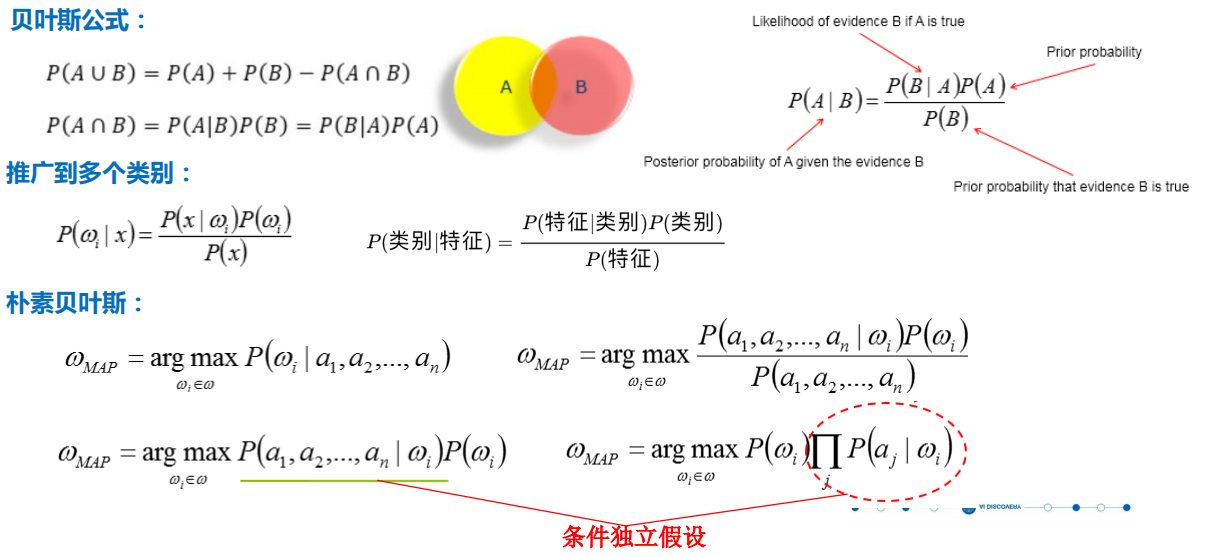

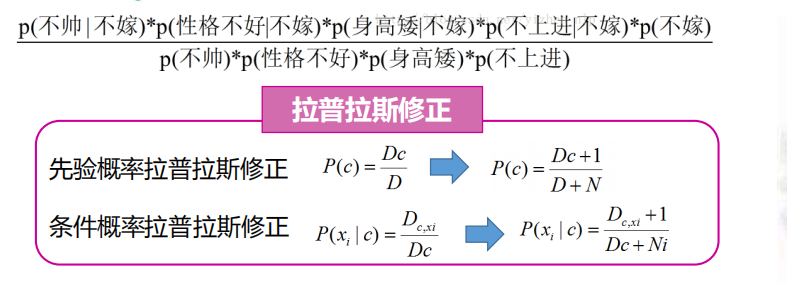






贝叶斯分类
举个栗子:一对男女朋友,男生向女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,
不上进,请你判断一下女生是嫁还是不嫁?

贝叶斯分类

优点:
(1) 算法逻辑简单,易于实现
(2)分类过程中时空开销小
缺点: 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总 是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往 是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
SVM(支持向量机)
在很久以前的情人节,大侠要去救他的爱人,但魔鬼和他玩了一个游戏。

再之后,人们把这些球叫做 「data」,把棍子叫做 「classifier」, 最大间隙trick 叫做 「optimization」, 拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。
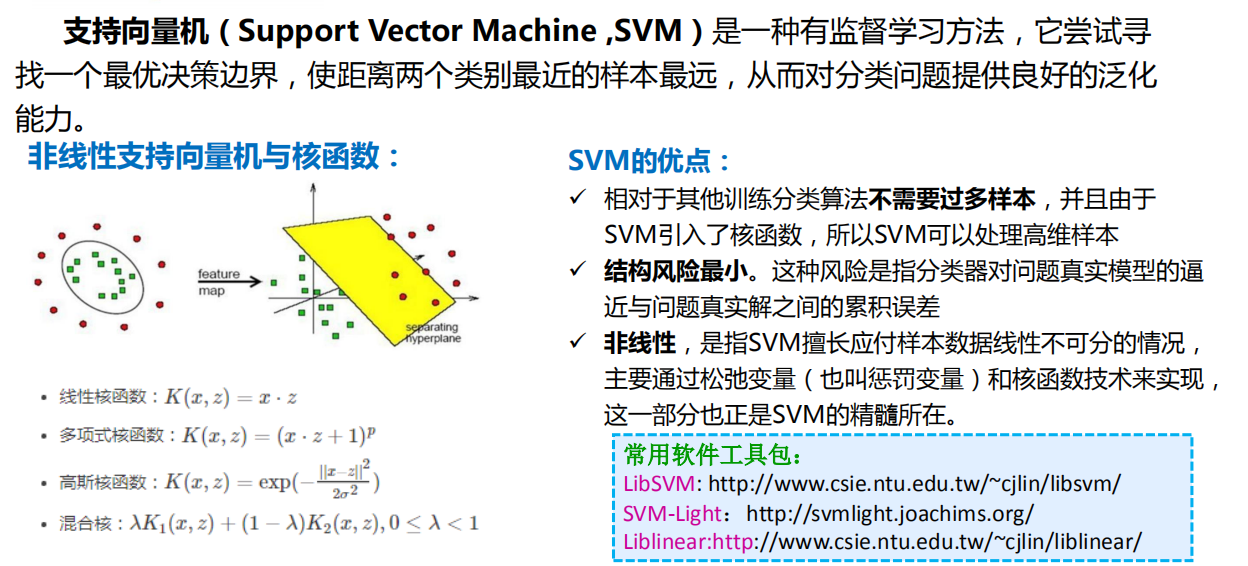
支持向量机(Support Vector Machine ) 是一种有监督学习方法,它尝试寻找一个最优决 策边界,使距离两个类别最近的样本最远。

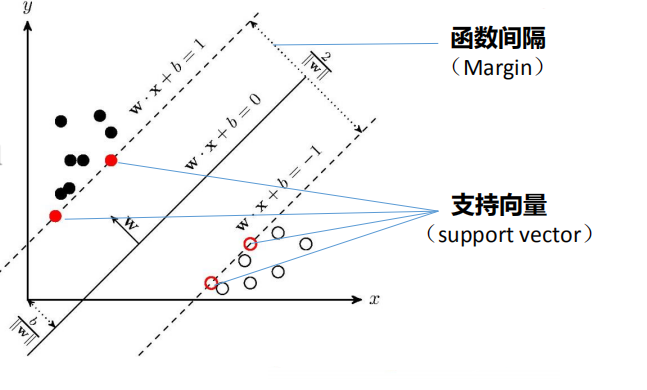
。

逻辑回归


最大熵模型

逻辑回归与最大熵模型

集成学习
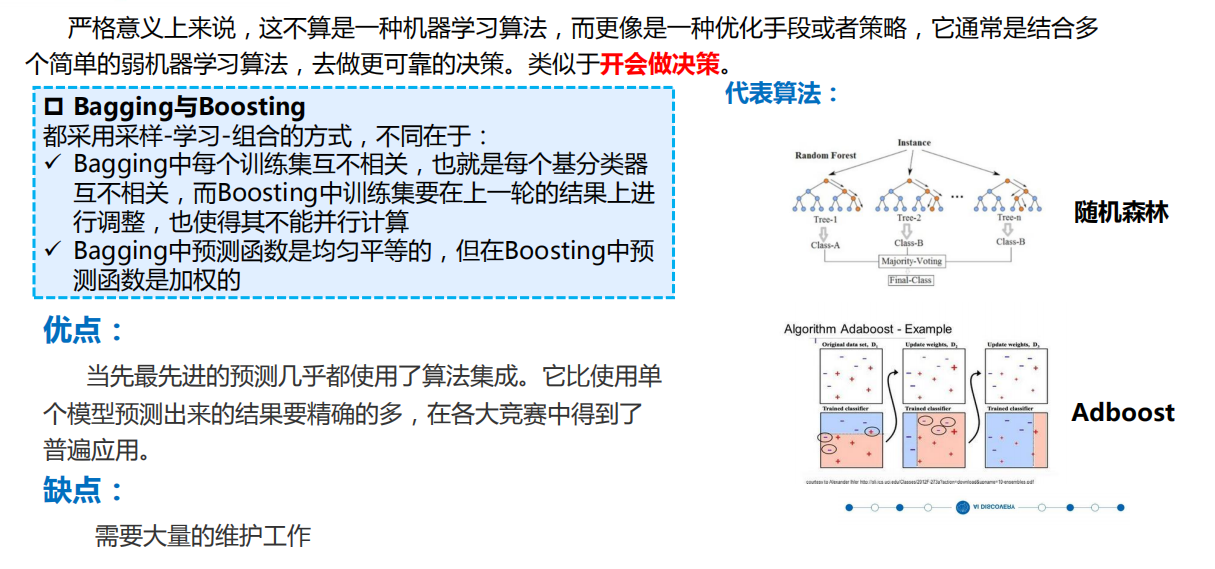
集成学习通过将多个弱分类器集成在一起,使它们共同完成学习任务,构建一个强分类器。潜在哲 学思想是“三个臭皮匠赛过诸葛亮”。
理论基础 两类集成方法 Bagging(bootstrap aggregating) Boosting(提升方法) 强可学习:在PAC学习框架中,一个概念,如果存在 存在一个多项式的学习算法能够学习它,并且正确率 很高,那么久称这个概念是强可学习的。 弱可学习:如果存在一个多项式的学习算法能够学习 它,学习的正确率金币随机猜测略好,那么就称这个 概念是弱可学习的。 Schapire证明强可学习与弱可学习是等价的,也 就是说,在PAC学习框架下,一个概念强可学习的充 分必要条件是这个概念若可学习的。