前言:
对弈类游戏的智能算法, 网上资料颇多, 大同小异. 我写这篇文章, 一方面是对当年的经典<<PC游戏编程(人机博弈)>>表达敬意, 另一方面, 也想对自己当年的游戏编程人生做下回顾.
上一篇博文:对弈类游戏的人工智能(1)--评估函数+博弈树算法, 着重讲述了评估函数+博弈树, 本文着重讲述学习算法, 以及性能优化和游戏性问题.

分析:
评估函数的引入, 为游戏AI提供了理论基础.
G(s) = a1 * f1(s) + a2 * f2(s) + ... + an * fn(s)
但评估函数的选定并非简单, 其面临的问题如下:
1). 评估因素的选择, 如何挑选, 因素是否越多越好
2). 对评估因素得分的归一化处理
3). 如何进行合理的权重系数分配
这些都是需要思考和优化的地方, 归纳而言就是特征(因素)选择, 权重系数学习.
有人提到了强化学习, 通过与环境的交互反馈来学习模型, 参见博文: "几种智能算法在黑白棋程序中的应用∗".
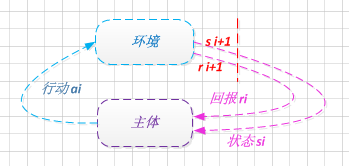
当然机器学习中的随机算法: 模拟退火/遗传算法, 也是有效的方式, 而且其更简单, 也更容易理解, 作者将在这边重点阐释.
遗传算法:
遗传算法(GA)是模拟自然界的进化过程而实现的."物竞天择, 适者生成"是其永恒的定律.
首先让我们来定义个体向量(染色体):
评估函数各个特征的权重系数构成权重向量 (a1, a2, a3, ..., an), 视为个体向量
其必须满足的约束如下:
• 权重向量中的系数和恒为1 (a1 + a2 + ... + an = 1)
• 经变异/交叉操作后, 系数权重和不为1, 则归一化过程统一为:
ai' = ai / ∑ ai (i = 0, 1, 2, ..., n)
再来定义操作子:
• 复制: 下一代拷贝上一代的权重系数向量即可
• 变异: 随机选定某个权重系数ai, 其值设定为某个(0~1)的随机值, 再进行归一化处理
• 交叉: 选定两个个体向量, 按概率进行对位权重系数交换, 再进行归一化处理.
适应度函数: 个体与其他个体的互相PK, 总得分即为其适应度值.
1). 初始阶段: 选择N个随机值的向量个体
2). 互相PK阶段: N个向量互相PK, 获取各自的适应度值
3). 进化阶段: 按适应度值排序, 引入淘汰率/变异率等, 进行复制/变异/交叉操作, 诞生新的N个个体
持续迭代2), 3)两阶段, 直到选取合适的个体.
该过程能达到我们的学习需求, 当然我们可以继续做如下优化:
• 引入陪跑员机制: 依经验挑选精英个体, 参加PK阶段, 用于评估个体的适应度, 但不参与进化(复制, 变异, 交叉)过程.
• 按适应值概率进化: 防止群体中极少数适应度高的个体被复制和遗传而达到局部最优解的情况.
复制/变异/交叉的比率, 以及群体数, 都会影响迭代次数和收敛效果.
总结:
使用遗传算法进行参数学习后, 可以合理地分配权重系数, 那事先说好的特征挑选呢? 简而言之, 通过筛选掉权重系数近似为0的特征即可, ^_^.
原本想继续讲下游戏AI的等级分类, 对博弈树的高级优化, 发现篇幅受限, 那就放到下一篇吧.
写在最后:
如果你觉得这篇文章对你有帮助, 请小小打赏下. 其实我想试试, 看看写博客能否给自己带来一点小小的收益. 无论多少, 都是对楼主一种由衷的肯定.
