1、方差是各个数据分别与其平均数之差的平方的和的平均数,用字母D表示。在概率论和数理统计中,方差(Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度。在许多实际问题中,研究变量和均值之间的偏离程度有着重要意义。
其中,x表示样本的平均数,n表示样本的数量,xi表示个体,而s^2就表示方差。用途:方差和期望的距离越大就越极端。
2、平方差公式(difference of two squares)是数学公式的一种,它属于乘法公式、因式分解及恒等式,被普遍使用。平方差指一个平方数或正方形,减去另一个平方数或正方形得来的乘法公式:a²-b²=(a+b)(a-b)
3、标准差(Standard Deviation) ,又常称均方差,但不同于均方误差(mean squared error,均方误差是各数据偏离真实值的距离平方的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,均方根误差才和标准差形式上接近),标准差是离均差平方和平均后的方根,用σ表示。假设有一组数值X1,X2,X3,......XN(皆为实数),其平均值(算术平均值)为μ,公式如图
4、均方误差(mean squared error,均方误差是各数据偏离真实值的距离平方的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,(加上根就是2)均方根误差才和标准差形式上接近):

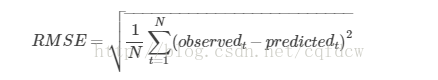
什么一范数二范数也是用来度量一个整体,比如两个个班的人比较高度,你可以用班里面最高的人(无穷范数)去比较,也可以用班里所有人的身高总和比较(一范数)https://blog.csdn.net/yangpan011/article/details/79461846

6.距离或相似度:
- 欧氏距离,参考https://blog.csdn.net/Kevin_cc98/article/details/73742037
- 标准化欧氏距离
- 马氏距离
- 夹角余弦距离,参考https://yq.aliyun.com/ziliao/425485
- 汉明距离
- 曼哈顿(Manhattan)距离
- 参考https://blog.csdn.net/Kevin_cc98/article/details/73742037
7. 正态分布(也叫高斯分布)
对于深度学习和机器学习工程师们来说,正态分布是世界上所有概率模型中最重要的一个。即使你没有参与过任何人工智能项目,也一定遇到过高斯模型,今天就让我们来看看高斯过程为什么这么受欢迎。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。https://baijiahao.baidu.com/s?id=1603586367690416158&wfr=spider&for=pc


