小组成员:信1201-1班 黄亚萍
信1201-1班 袁亚姣
一、题目要求
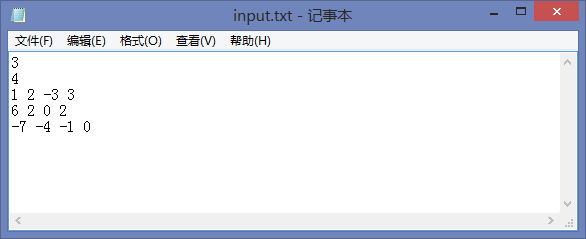
程序要使用的数组放在一个叫 input.txt 的文件中, 文件格式是:
数组的行数,
数组的列数,
每一行的元素, (用逗号分开)
每一个数字都是有符号32位整数, 当然, 行数和列数都是正整数。
二、设计思路
在结对开发之体验中一维数组的子数组的和的最大值的基础上加以拓展:
(1)当子数组的维数为1时,在M*N的数组中有M个子数组,直接用一维数组的处理办法求出其最大值;
(2)当子数组的维数不为1时,第i行和第i+1行元素对应求和的方式,重新得到新的数组,重复(1)的操作,直到子数组就是原来的数组本身为止。
三、程序源代码
1 #include"stdafx.h" 2 #include <iostream> 3 #include <fstream> 4 using namespace std; 5 # define M 100 6 # define N 100 7 int hang1=0; 8 int hang2=0; 9 int lie1=0; 10 int lie2=0; 11 int maxx = -100; 12 int sum1(int k,int a[],int number) //一维数组行数元素求和 13 { 14 int x=0; 15 for(int i=k;i<=number+k-1;i++) //数组元素的个数为number 16 { 17 x=x+a[i]; 18 } 19 return x; 20 } 21 int sum2(int k,int a[M][N],int number,int num) //二维数组列数元素求和 22 { 23 int x=0; 24 for(int i=k;i<=number+k-1;i++) 25 { 26 x=x+a[i][num]; 27 } 28 return x; 29 } 30 int Largest1(int list[],int length) //一维数组求数组的子数组的和的最大值 31 { 32 int sum[N]; 33 int i,j,max=-100; 34 for(i=1;i<=length;i++) //元素个数为i 35 { 36 for(j=1;j<=length-i+1;j++) //子数组的第j个元素,求最大值 37 { 38 sum[j]=sum1(j,list,i); 39 if(sum[j]>=max) 40 { 41 max=sum[j]; 42 } 43 } 44 } 45 return max; 46 } 47 48 void Largest3(int list[],int length) 49 { 50 int sum[N]; 51 int i,j; 52 for(i=1;i<=length;i++) 53 { 54 for(j=1;j<=length-i+1;j++) 55 { 56 sum[j]=sum1(j,list,i); 57 if(sum[j]>= maxx) 58 { 59 maxx=sum[j]; 60 lie1 = j; 61 lie2 = j+i-1; 62 } 63 } 64 } 65 } 66 67 int Largest2(int list[M][N],int number_x,int number_y) //二维数组求数组的子数组的和的最大值 68 { 69 int max,m; 70 int max2[N]; 71 int sum[M][N]; 72 int max3[N]; 73 for(int i=1;i<=number_x;i++) //数组行数为i 74 { 75 cout<<"子数组行数为"<<i<<","<<endl; 76 77 for(m=1;m<=number_x-i+1;m++) //子数组的第一行为原数组的第m行 78 { 79 cout<<" 第"<< m <<"行的最大值为:"; 80 for(int j=1;j<=number_y;j++) //子数组第j列元素 81 { 82 sum[i][j]=sum2(m,list,i,j); 83 } 84 Largest3(sum[i],number_y); 85 max2[m]=Largest1(sum[i],number_y); //数行数为i时子数组第m行的最大值 86 cout<<max2[m]<<endl; 87 max3[i]=max2[1]; 88 for(int k=1;k<=i;k++) 89 { 90 if(max2[k]>=max3[i]) 91 { 92 max3[i]=max2[k]; 93 hang1=m; 94 } 95 } 96 } 97 } 98 max=max3[1]; 99 for(int n=1;n<=number_x;n++) 100 { 101 if(max3[n]>=max) 102 { 103 max=max3[n]; 104 hang1=m; 105 hang2=n; //子数组的行数为第m行到第m+n行 106 107 } 108 } 109 return max; 110 } 111 void show(int arry[N][N],int length1,int length2) //输出矩阵 112 { 113 for(int i=1;i<=length1;i++) 114 { 115 for(int j=1;j<=length2;j++) 116 { 117 cout<<arry[i][j]<<" "; 118 } 119 cout<<endl; 120 } 121 } 122 int main(int argc, char* argv[]) 123 { 124 int i,number_hang,number_lie; 125 int list[M][N]; 126 127 ifstream infile("input.txt"); 128 if(!infile) 129 cout<<"读取失败!"<<endl; 130 else 131 { 132 infile>>number_hang>>number_lie; 133 for(int i=1;i<=number_hang;i++) 134 { 135 for(int j=1;j<=number_lie;j++) 136 { 137 infile>>list[i][j]; 138 } 139 } 140 } 141 142 cout<<"以矩阵形式展示为:"<<endl; 143 show(list,number_hang,number_lie); 144 cout<<endl; 145 cout<<"最大值为:"<<Largest2(list,number_hang,number_lie)<<endl; 146 cout<<endl; 147 cout<<"对应的最大值的子数组为:"<<endl; 148 149 for(i=hang1-1;i<hang2+hang1-1;i++) 150 { 151 for(int j=lie1;j<=lie2;j++) 152 { 153 cout<<list[i][j]<<" "; 154 } 155 cout<<endl; 156 } 157 cout<<endl; 158 return 0; 159 }
四、结果截图

五、实验总结
本次实验是在上次结对开发的实验基础上进一步加工完善的,在完成的过程中,和队员一起构思完成设计思路与过程,让我了解到完成一个项目,只有先缕清思路,有一个清晰明白的流程,才能顺利的完成代码的编辑,调试,测试与结尾,才能达到事半功倍的效果;以前学习的过程中,拿到一个题目就开始敲代码,往往忽略了最重要的构思与设计部分,提示我们做事之前一定要有条理,不可盲目。
附件:
