Description
Word puzzles are usually simple and very entertaining for all ages. They are so entertaining that Pizza-Hut company started using table covers with word puzzles printed on them, possibly with the intent to minimise their client's
perception of any possible delay in bringing them their order.
Even though word puzzles may be entertaining to solve by hand, they may become boring when they get very large. Computers do not yet get bored in solving tasks, therefore we thought you could devise a program to speedup (hopefully!) solution finding in such puzzles.
The following figure illustrates the PizzaHut puzzle. The names of the pizzas to be found in the puzzle are: MARGARITA, ALEMA, BARBECUE, TROPICAL, SUPREMA, LOUISIANA, CHEESEHAM, EUROPA, HAVAIANA, CAMPONESA.
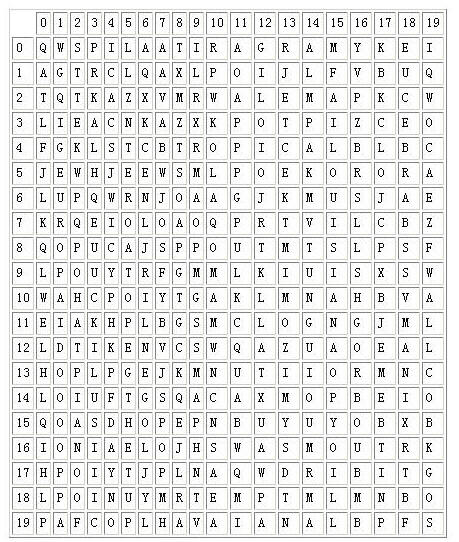
Your task is to produce a program that given the word puzzle and words to be found in the puzzle, determines, for each word, the position of the first letter and its orientation in the puzzle.
You can assume that the left upper corner of the puzzle is the origin, (0,0). Furthemore, the orientation of the word is marked clockwise starting with letter A for north (note: there are 8 possible directions in total).
Even though word puzzles may be entertaining to solve by hand, they may become boring when they get very large. Computers do not yet get bored in solving tasks, therefore we thought you could devise a program to speedup (hopefully!) solution finding in such puzzles.
The following figure illustrates the PizzaHut puzzle. The names of the pizzas to be found in the puzzle are: MARGARITA, ALEMA, BARBECUE, TROPICAL, SUPREMA, LOUISIANA, CHEESEHAM, EUROPA, HAVAIANA, CAMPONESA.

Your task is to produce a program that given the word puzzle and words to be found in the puzzle, determines, for each word, the position of the first letter and its orientation in the puzzle.
You can assume that the left upper corner of the puzzle is the origin, (0,0). Furthemore, the orientation of the word is marked clockwise starting with letter A for north (note: there are 8 possible directions in total).
Input
The first line of input consists of three positive numbers, the number of lines, 0 < L <= 1000, the number of columns, 0 < C <= 1000, and the number of words to be found, 0 < W <= 1000. The following L input lines, each one of
size C characters, contain the word puzzle. Then at last the W words are input one per line.
Output
Your program should output, for each word (using the same order as the words were input) a triplet defining the coordinates, line and column, where the first letter of the word appears, followed by a letter indicating the orientation
of the word according to the rules define above. Each value in the triplet must be separated by one space only.
Sample Input
20 20 10 QWSPILAATIRAGRAMYKEI AGTRCLQAXLPOIJLFVBUQ TQTKAZXVMRWALEMAPKCW LIEACNKAZXKPOTPIZCEO FGKLSTCBTROPICALBLBC JEWHJEEWSMLPOEKORORA LUPQWRNJOAAGJKMUSJAE KRQEIOLOAOQPRTVILCBZ QOPUCAJSPPOUTMTSLPSF LPOUYTRFGMMLKIUISXSW WAHCPOIYTGAKLMNAHBVA EIAKHPLBGSMCLOGNGJML LDTIKENVCSWQAZUAOEAL HOPLPGEJKMNUTIIORMNC LOIUFTGSQACAXMOPBEIO QOASDHOPEPNBUYUYOBXB IONIAELOJHSWASMOUTRK HPOIYTJPLNAQWDRIBITG LPOINUYMRTEMPTMLMNBO PAFCOPLHAVAIANALBPFS MARGARITA ALEMA BARBECUE TROPICAL SUPREMA LOUISIANA CHEESEHAM EUROPA HAVAIANA CAMPONESA
Sample Output
0 15 G 2 11 C 7 18 A 4 8 C 16 13 B 4 15 E 10 3 D 5 1 E 19 7 C 11 11 H
Source
1、Trie树暴搜,能够说是Trie模板题。将单词插入Trie树后,以地图上每一个点作为起点,8个方向搜索单词就可以,WA了6发,总算AC了。须要注意的就是当眼下的单词已经搜到尽头(终止节点),不要停止搜索!
#include <stdio.h>
#include <iostream>
#include <string>
#include <string.h>
#define WORD 26
#define MAXN 1050
using namespace std;
struct trie
{
trie *child[WORD]; //儿子节点指针
int id; //若该节点为某单词的终止节点,id=该单词编号
trie(){
memset(child,0,sizeof(child)); //儿子节点初始化为空
id=-1;
}
}; //root=根节点
trie *root=new trie();
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1}; //搜索方向,暴力枚举每一个点八个方向
int ans[MAXN][3],visit[MAXN],L,C,W; //第i个单词的位置=(ans[i][1],ans[i][2]),方向为ans[i][0]
string c[MAXN],word; //保存全部字符串的矩阵
void build(string s,int num) //将编号为num的字符串s插入trie树中
{
int i;
trie *p=root; //初始时p指向根节点
for(i=0;i<s.size();i++)
{
if(p->child[s[i]-'A']==NULL) //无现成的字符串相应位置儿子节点
p->child[s[i]-'A']=new trie();
p=p->child[s[i]-'A']; //将指针移向当前节点以下的相应儿子节点
}
p->id=num; //记下终止节点的相应单词编号
}
void search(int sx,int sy,int dir) //搜索trie树,单词起点(sx,sy),延伸方向为dir
{
int xx=sx,yy=sy; //当前单词字母的坐标(xx,yy)
trie *point=root; //point指向当前trie树的节点
while(xx>=0&&xx<L&&yy>=0&&yy<C) //坐标未越界
{
if(!point->child[c[xx][yy]-'A']) //到达了终止节点,但单词还没结束
break;
else
point=point->child[c[xx][yy]-'A']; //指针向该节点下方移动
if(point->id!=-1) //该节点为终止节点
{
if(visit[point->id]==0)
{
visit[point->id]=1;
ans[point->id][0]=dir; //记录下该单词的開始坐标、方向
ans[point->id][1]=sx;
ans[point->id][2]=sy;
}
}
xx+=dx[dir]; //移动坐标
yy+=dy[dir];
}
}
int main()
{
int i,j,k;
scanf("%d%d%d",&L,&C,&W);
for(i=0;i<L;i++)
{
cin>>c[i];
}
for(i=0;i<W;i++)
{
cin>>word;
build(word,i); //将单词插入trie树
}
for(i=0;i<L;i++) //枚举起点(i,j)
for(j=0;j<C;j++)
for(k=0;k<8;k++) //暴力枚举单词存在的方向
search(i,j,k);
for(i=0;i<W;i++)
printf("%d %d %c
",ans[i][1],ans[i][2],ans[i][0]+'A');
return 0;
}
2、AC自己主动机。Trie树暴力的方法由于是从地图上每一个点開始搜,并且Trie树失配后就必须回到根节点又一次来过,所以复杂度太高。能够直接用AC自己主动机,利用AC自己主动机能够将字符串的后缀和模式串匹配的特点,从地图的四个边上的点作为起点,向八个方向匹配就可以。加之匹配过程中失配后能够沿着失败指针向上走,不必直接到根节点重头来,因此复杂度比第一种方法低不少,可是代码也太长太复杂(140行)
#include <stdio.h>
#include <iostream>
#include <queue>
#include <string>
#include <string.h>
#define WORD 26
#define MAXN 1050
using namespace std;
struct trie
{
trie *child[WORD]; //儿子节点指针
trie *fail; //失败指针(前缀指针)
int id; //若该节点为某单词的终止节点,id=该单词编号
trie()
{
memset(child,0,sizeof(child)); //儿子节点初始化为空
fail=NULL;
id=-1;
}
}tree[MAXN*100]; //root=根节点
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1}; //搜索方向,暴力枚举每一个点八个方向
int ans[MAXN][3],len[MAXN],L,C,W,nNodesCount=0; //第i个单词的位置=(ans[i][1],ans[i][2]),方向为ans[i][0],nNodeCounts=节点个数
string c[MAXN],word; //保存全部字符串的矩阵
void build(trie *pRoot,string s,int num) //将编号为num的字符串s插入树根为pRoot的trie树中
{
int i;
len[num]=s.size();
for(i=0;s[i];i++)
{
if(pRoot->child[s[i]-'A']==NULL) //无现成的字符串相应位置儿子节点
{
pRoot->child[s[i]-'A']=tree+nNodesCount;
nNodesCount++; //节点个数+1
}
pRoot=pRoot->child[s[i]-'A']; //将指针移向当前节点以下的相应儿子节点
}
pRoot->id=num; //记下终止节点的相应单词编号
}
void acAutomation() //搭建前缀指针。构造AC自己主动机
{
int i;
for(i=0;i<WORD;i++)
tree[0].child[i]=tree+1; //让第0个节点的全部儿子节点都指向第一个节点,即不论什么单词都能从根节点匹配下去
tree[0].fail=NULL; //根节点的失败指针指向空
tree[1].fail=tree; //第一个节点的失败指针指向根节点
trie *pRoot,*point;
queue<trie*>q;
q.push(tree+1); //将第一个节点入队
while(!q.empty()) //队列不为空
{
pRoot=q.front();
q.pop(); //队首出队
for(i=0;i<WORD;i++) //遍历该节点的儿子
{
point=pRoot->child[i]; //point=单词当前字母相应的儿子
if(point)
{
trie *pPrev=pRoot->fail; //失败指针指向的节点
while(pPrev) //当指向的节点不为空,不断向上爬
{
if(pPrev->child[i]) //指向的节点能匹配
{
point->fail=pPrev->child[i]; //将该节点的失败指针指向失败指针指向的节点的能够匹配的儿子节点
break;
}
else
pPrev=pPrev->fail; //无法匹配,向该失败指针指向的节点的失败指针往上爬
}
q.push(point); //该节点入队
}
}
}
}
void ACsearch(int sx,int sy,int dir) //搜索,单词起点(sx,sy),延伸方向为dir
{
int i,xx=sx,yy=sy;
trie *point=tree+1;
while(xx>=0&&xx<L&&yy>=0&&yy<C)
{
while(1)
{
if(point->child[c[xx][yy]-'A']) //该节点的儿子节点能够匹配
{
point=point->child[c[xx][yy]-'A']; //指针向儿子移动
if(point->id!=-1) //指针相应节点为危急节点,则匹配成功,记录答案
{
ans[point->id][0]=dir; //记录下该单词的開始坐标、方向
ans[point->id][1]=xx-(len[point->id]-1)*dx[dir];
ans[point->id][2]=yy-(len[point->id]-1)*dy[dir];
}
break;
}
else
point=point->fail; //否则,无法匹配,向失败指针移动
}
xx+=dx[dir];
yy+=dy[dir];
}
}
int main()
{
int i,j,k;
nNodesCount=2;
scanf("%d%d%d",&L,&C,&W);
for(i=0;i<L;i++) cin>>c[i];
for(i=0;i<W;i++)
{
cin>>word;
build(tree+1,word,i); //将单词插入trie树
}
acAutomation(); //插入失败指针,构造AC自己主动机
for(i=0;i<L;i++)
for(j=0;j<8;j++)
ACsearch(i,0,j);
for(i=0;i<L;i++)
for(j=0;j<8;j++)
ACsearch(i,C-1,j);
for(i=0;i<C;i++)
for(j=0;j<8;j++)
ACsearch(0,i,j);
for(i=0;i<C;i++)
for(j=0;j<8;j++)
ACsearch(L-1,i,j);
for(i=0;i<W;i++)
printf("%d %d %c
",ans[i][1],ans[i][2],ans[i][0]+'A');
return 0;
}