图像切割—基于图的图像切割(Graph-Based Image Segmentation)
Reference:
Efficient Graph-Based Image Segmentation,IJCV 2004,MIT Code
最后一个暑假了,不打算开疆辟土了。战略中心转移到品味经典。计划把图像切割和目标追踪的经典算法都看一看。再记些笔记。
Graph-Based Segmentation 是经典的图像切割算法,作者Felzenszwalb也是提出DPM算法的大牛。该算法是基于图的贪心聚类算法,实现简单。速度比較快,精度也还行。
只是。眼下直接用它做切割的应该比較少,毕竟是99年的跨世纪元老,可是非常多算法用它作垫脚石。比方Object Propose的开山之作《Segmentation as Selective Search for Object Recognition》就用它来产生过切割(oversegmentation)。还有的语义切割(senmatic segmentation )算法用它来产生超像素(superpixels)详细忘记了……
图的基本概念
由于该算法是将照片用加权图抽象化表示,所以补充图的一些基本概念。
图是由顶点集 (vertices)和边集
(vertices)和边集 (edges)组成,表示为
(edges)组成,表示为 。顶点
。顶点 ,在本文中即为单个的像素点。连接一对顶点的边
,在本文中即为单个的像素点。连接一对顶点的边 具有权重
具有权重 ,本文中的意义为顶点之间的不相似度,所用的是无向图。
,本文中的意义为顶点之间的不相似度,所用的是无向图。

树:特殊的图。图中随意两个顶点,都有路径相连接,可是没有回路。如上图中加粗的边所连接而成的图。假设看成一团乱连的珠子,仅仅保留树中的珠子和连线。那么随便选个珠子,都能把这棵树中全部的珠子都提起来。假设,i和h这条边也保留下来。那么顶点h,i,c,f,g就构成了一个回路。
最小生成树(MST, minimum spanning tree):特殊的树。给定须要连接的顶点,选择边权之和最小的树。
上图即是一棵MST

本文中,初始化时每个像素点都是一个顶点,然后逐渐合并得到一个区域,确切地说是连接这个区域中的像素点的一个MST。如图,棕色圆圈为顶点。线段为边。合并棕色顶点所生成的MST,相应的就是一个切割区域。切割后的结果事实上就是森林。
相似性
既然是聚类算法,那应该根据何种规则判定何时该合二为一,何时该继续划清界限呢?
对于孤立的两个像素点,所不同的是颜色,自然就用颜色的距离来衡量两点的相似性,本文中是使用RGB的距离,即
当然也能够用perceptually uniform的Luv或者Lab色彩空间,对于灰度图像就仅仅能使用亮度值了,此外。还能够先使用纹理特征滤波,再计算距离,比方,先做Census Transform再计算Hamming distance距离。
全局阈值à自适应阈值
上面提到应该用亮度值之差来衡量两个像素点之间的差异性。对于两个区域(子图)或者一个区域和一个像素点的相似性,最简单的方法即仅仅考虑连接二者的边的不相似度。

如图,已经形成了棕色和绿色两个区域,如今通过紫色边来推断这两个区域是否合并。
那么我们就能够设定一个阈值,当两个像素之间的差异(即不相似度)小于该值时,合二为一。
迭代合并,终于就会合并成一个个区域。效果类似于区域生长:星星之火,能够燎原。


显然,上面这张图应该聚成右图所思的3类,高频区h,斜坡区s,平坦区p。
假设我们设置一个全局阈值。那么假设h区要合并成一块的话,那么该阈值要选非常大。可是那样就会把p和s区域也包括进来。切割结果太粗。假设以p为參考,那么阈值应该选特别小的值,那样的话。p区是会合并成一块。可是,h区就会合并成特别特别多的小块,如同一面支离破碎的镜子,切割结果太细。
显然,全局阈值并不合适,那么自然就得用自适应阈值。对于p区该阈值要特别小,s区稍大。h区巨大。
对于两个区域(原文中叫Component,实质上是一个MST,单独的一个像素点也能够看成一个区域),本文使用了很直观,但抗干扰性并不强的方法。先来两个定义。原文根据这两个附加信息来得到自适应阈值。
一个区域的类内差异 :
:

能够近似理解为一个区域内部最大的亮度差异值,定义是MST中不相似度最大的一条边。
两个区域的类间差异 :
:

即连接两个区域全部边中,不相似度最小的边的不相似度,也就是两个区域最相似的地方的不相似度。
那么直观的推断是否合并的标准:

等价条件

解释:  ,
, 各自是区域
各自是区域 和
和 所能忍受的最大差异,当二者都能忍受当前差异
所能忍受的最大差异,当二者都能忍受当前差异 时。你情我愿,一拍即合,仅仅要有一方不愿意,就不能强求。
时。你情我愿,一拍即合,仅仅要有一方不愿意,就不能强求。
特殊情况。当二者都是孤立的像素值时。 ,全部像素都是"零容忍"仅仅有像素值全然一样才干合并。自然会导致过切割。所以刚開始的时候,应该给每一个像素点设定一个能够容忍的范围。当生长到一定程度时。就应该去掉该初始容忍值的作用。
,全部像素都是"零容忍"仅仅有像素值全然一样才干合并。自然会导致过切割。所以刚開始的时候,应该给每一个像素点设定一个能够容忍的范围。当生长到一定程度时。就应该去掉该初始容忍值的作用。
原文条件例如以下
 添加项
添加项 :
:

当中 为区域
为区域 所包括的像素点的个数,如此。随着区域逐渐扩大,这一项的作用就越来越小,最后差点儿能够忽略不计。那么
所包括的像素点的个数,如此。随着区域逐渐扩大,这一项的作用就越来越小,最后差点儿能够忽略不计。那么 就是一个能够控制所形成的的区域的大小,假设。
就是一个能够控制所形成的的区域的大小,假设。 那么,差点儿每一个像素都成为了一个独立的区域,假设
那么,差点儿每一个像素都成为了一个独立的区域,假设 ,显然整张图片都会聚成一块。所以,
,显然整张图片都会聚成一块。所以,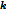 越大。切割后的图片也就越大。
越大。切割后的图片也就越大。
当然,能够採用中位数来应对超调,只是这就变成了一个NP难问题。证明见原文
形状相似
前面提到的用颜色信息来聚类,改动相似性衡量标准,能够聚类成我们想要的特定形状。
比方我们希望得到非常多长条形的区域,那么能够用聚类后的所形成的区域的面积/周长 + 亮度值的差 衡量两个子图或者两个像素之间的相似度。
由于长条形的面积/周长会比較小。
算法步骤
Step 1: 计算每个像素点与其8邻域或4邻域的不相似度。

如左边所看到的,实线为仅仅计算4领域。加上虚线就是计算8邻域。因为是无向图,依照从左到右。从上到下的顺序计算的话。仅仅须要计算右图中灰色的线就可以。
Step 2: 将边依照不相似度non-decreasing排列(从小到大)排序得到 。
。
Step 3: 选择
Step 4: 对当前选择的边 进行合并推断。设其所连接的顶点为
进行合并推断。设其所连接的顶点为 。假设满足合并条件:
。假设满足合并条件:
(1) 不属于同一个区域
不属于同一个区域 ;
;
(2)不相似度不大于二者内部的不相似度。
 则运行Step 5。否则运行Step 6
则运行Step 5。否则运行Step 6
Step 5: 更新阈值以及类标号。
更新类标号:将 的类标号统一为
的类标号统一为 的标号。
的标号。
更新该类的不相似度阈值为: 。
。
注意:因为不相似度小的边先合并,所以。 即为当前合并后的区域的最大的边,即
即为当前合并后的区域的最大的边,即 。
。
Step 6: 假设 ,则依照排好的顺序。选择下一条边转到Step 4,否则结束。
,则依照排好的顺序。选择下一条边转到Step 4,否则结束。
结果



Segmentation parameters: sigma = 0.5, k= 500, min = 50.
Sigma:先对原图像进行高斯滤波去噪。sigma即为高斯核的
k: 控制合并后的区域的大小,见前文
min: 后处理參数,切割后会有非常多小区域,当区域 像素点的个数
像素点的个数 小于min时。选择与其差异最小的区域
小于min时。选择与其差异最小的区域 合并即
合并即 。
。
性质讨论
结果尽管不是非常好,但有非常好的全局性质。结论非常有意思,有兴趣的能够看看。
首先要说明的是,对于不论什么图像,始终存在一种切割方法,使得切割的结果既只是细。也只是粗。
可是并不唯一。
引理
假设step 4
时, ,但并没有合并,即
,但并没有合并,即 ,那么肯定有一个区域已经切割好了,比方
,那么肯定有一个区域已经切割好了,比方 ,那么区域
,那么区域 的范围就不会再有添加,它将会成为终于的切割区域中的一个区域。
的范围就不会再有添加,它将会成为终于的切割区域中的一个区域。
Proof:
如果。 ,因为边是依照non-decreasing排序。所以剩下的连接
,因为边是依照non-decreasing排序。所以剩下的连接 的边的不相似度肯定都不低于
的边的不相似度肯定都不低于 。最小的边都不行,其余的边自然是靠边站了。
。最小的边都不行,其余的边自然是靠边站了。
只是,原文说仅仅能仅仅有一个已经切割好了。可是我认为另一种情况。 而且
而且 ,那么这两个区都应该分好了才对呀。
,那么这两个区都应该分好了才对呀。
Not Too fine
切割太细,也就是本来不应该分开的区域被拦腰截断。可是本算法是能保证有情人终成眷属的,绝对不会干棒打鸳鸯拆散一对是一对的事。
Proof:

反证法:如上图。本不应该切割,则应该满足条件 。如果分开了,那么必然存在一条边
。如果分开了,那么必然存在一条边 导致二者没有合并。那么由前面的引理,必然存在一个区域成为终于切割结果的一部分,如果为A部分,再回溯到推断这条边的时候。必然有。
导致二者没有合并。那么由前面的引理,必然存在一个区域成为终于切割结果的一部分,如果为A部分,再回溯到推断这条边的时候。必然有。 ,从而
,从而 ,因为是按non-decreasing
顺序,所以A部分和B部分最小的边就是
,因为是按non-decreasing
顺序,所以A部分和B部分最小的边就是 ,那么
,那么 与如果条件矛盾。
与如果条件矛盾。
Not Too coarse
切割太粗。也就是本应该分开的区域没有分开。但本算法能保证当断则断。不会藕断丝连。
反证法:如上图。本应该切割,则应满足条件 。如果还是
。如果还是 ,
, 为连接A,B最小的边。如果合并了,因为
为连接A,B最小的边。如果合并了,因为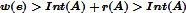 。并且是non-decreasing
顺序,所以在判定边
。并且是non-decreasing
顺序,所以在判定边 之前A区域已经形成。
之前A区域已经形成。
假设切割过粗。则判定这条边时最小的边满足 ,则必然
,则必然 使得二者合并了。
使得二者合并了。
和条件矛盾。
等权边处理先后次序的影响
假设两条边 。
。 的权值同样,那么排序时候。谁排前头。谁落后面有影响吗?结论是木有。
的权值同样,那么排序时候。谁排前头。谁落后面有影响吗?结论是木有。
Proof:
Case1: ,
, 连接的区域同样,即
连接的区域同样,即 ,
,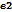 连接的都是区域
连接的都是区域 。那么它俩谁在前面都没关系。
。那么它俩谁在前面都没关系。
Case2: ,
, 连接的区域全然不同,比方
连接的区域全然不同,比方 连接区域,
连接区域, ,
, 连接区域
连接区域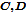 ,那么谁先谁后,都不影响
,那么谁先谁后,都不影响 是否合并,也不影响
是否合并,也不影响 是否合并。
是否合并。
Case3: 连接
连接 ,
, 连接
连接
Case3-1: 在先。
在先。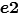 在后,而且,
在后,而且, 使得
使得 合并。交换二者处理顺序。先处理
合并。交换二者处理顺序。先处理 。后处理
。后处理 。
。
假设 不合并
不合并 ,那不影响
,那不影响 合并
合并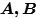 ;假设
;假设 合并
合并 ,那么合并后的
,那么合并后的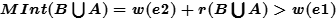 ,照样合并。
,照样合并。
Case3-2: 在先,
在先, 在后,而且,
在后,而且,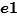 不合并
不合并 ,交换二者处理顺序。先处理
,交换二者处理顺序。先处理 ,后处理
,后处理 。假设是
。假设是 。
。
那 是否合并
是否合并 。都不会使得
。都不会使得 合并;假设
合并;假设 ,那相同也有
,那相同也有 ,相同也没影响。
,相同也没影响。
补充:
彩色图片
对于彩色图片,上文是将R,G,B作为距离。整张图片仅仅进行一次切割。原文说对每个通道都进行一次切割,最后对结果取交集,也就是说图片中的两个点要划分到同一个区域,则在R,G,B三个通道的划分结果中。它俩得始终在同一个区域。原文说这样效果更好……只是他的程序是採用一次切割。
Nearest Neighbor Graphs
前文是仅仅用了空间位置 来构件图的连接关系,缺点是明显的,空间不相邻,色彩全然一样也白搭,于是中间略微有断开都会分成多个部分。于是还有一种更为平等的策略是二者一块考虑,先映射到特征空间
来构件图的连接关系,缺点是明显的,空间不相邻,色彩全然一样也白搭,于是中间略微有断开都会分成多个部分。于是还有一种更为平等的策略是二者一块考虑,先映射到特征空间 。再构建图。此时有连接关系的就不一定是4/8邻域了,因为有
。再构建图。此时有连接关系的就不一定是4/8邻域了,因为有 对边。因此假设考虑全部边的连接关系的话,太恐怖了!原文是对每一个像素点找10个欧氏距离近期的点即10近期邻。构建图。当然。第二种方法不是固定邻居数目,而是限定距离范围。
对边。因此假设考虑全部边的连接关系的话,太恐怖了!原文是对每一个像素点找10个欧氏距离近期的点即10近期邻。构建图。当然。第二种方法不是固定邻居数目,而是限定距离范围。
那么类内距离 的解释就和直观了。类内最短的距离,那么会以这条边为半径,在特征空间构成一个超球体,只是会和别人有相交。
的解释就和直观了。类内最短的距离,那么会以这条边为半径,在特征空间构成一个超球体,只是会和别人有相交。
 相同还是两个类直接的最短距离。
相同还是两个类直接的最短距离。
找10-NN太累,原文採用近似算法ANN《Approximate nearest neighbor searching》来找10近邻。快。
剩下的和上面一样,可是有一点我没明确,就是 的更新,比方上图。肯定是用绿色这条线更新,那么
的更新,比方上图。肯定是用绿色这条线更新,那么 的意义就不再是包括集合全部点的最短半径了,求解?
的意义就不再是包括集合全部点的最短半径了,求解?
结果例如以下:能够看到被栏杆分开的草地也连在一块了,以下的花朵也属于同一个类别


下个星期写Mean shift,敬请期待
