Gradient Computing
前面我们介绍过分类器模型一般包含两大部分,一部分是score function,将输入的原始数据映射到每一类的score,另外一个重要组成部分是loss function,计算预测值
与实际值之间的误差,具体地,给定一个线性分类函数:f(xi;W)=Wxi,我们定义如下的loss function:
L=1N∑i∑j≠yi[max(0,f(xi,W)j−f(xi,W)yi+1)]+αR(W)
我们看到
L与参数
W有关,所以我们需要找到一个合适的
W使得
L尽可能小,这个过程称为优化。所以一个完整的分类模型,包括三个核心部分:score function,loss function 以及optimization(优化)。
一般来说,我们定义的loss function中,里面涉及的输入变量都是高维的向量,要让它们直接可视化是不可能的,我们可以通过低维的情况下得到一些直观的印象,让loss在直线或者平面上变化,比如
我们可以先初始化一个权值矩阵W,然后让该矩阵沿着方向W1变化,那么可以评估W1不同的幅值对loss的影响,即L(W+aW1),这个loss会随着不同的a生成
一条曲线,同样,我们可以让L在两个方向W1,W2变化,L(W+aW1)+bW2不同的a,b会生成不同的loss,这个loss会形成一个平面,如下图所示:
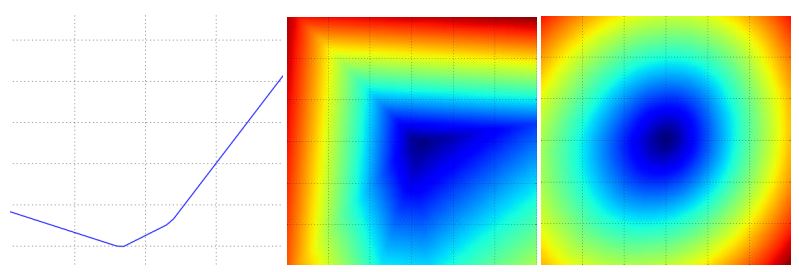
我们可以通过从数学的角度解释这个loss function,考虑只有一个样本的情况,我们有:
Li=∑j≠yi[max(0,wTjxi−wTyixi+1)]
从这个表达式可以看出,样本的loss是W的一个线性函数,如果我们考虑一个含有三个样本(每个样本是一个一维的点)的训练集,这个训练集有三个类别,那么训练集
的loss可以表示为:
L0=[max(0,wT1x0−wT0x0+1)]+[max(0,wT2x0−wT0x0+1)]L1=[max(0,wT0x1−wT1x1+1)]+[max(0,wT2x1−wT1x1+1)]L2=[max(0,wT0x2−wT2x2+1)]+[max(0,wT1x2−wT2x2+1)]L=(L0+L1+L2)/3
因为样本
xi是一维的,所以系数
wi也是一维的,它们的和
L与与
W的关系可以由下图表示:
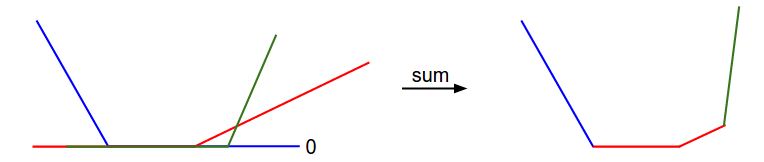
上图给出的是一维的情况,如果是高维的话,这个要复杂的多,我们希望找到一个W使得该loss最小,上图是一个凸函数,对于这类函数的优化,是一大类属于凸优化的
问题,但是我们后面介绍的神经网络,其loss function是比这更复杂的一类函数,不是单纯地凸函数。上面的图形告诉我们这个loss function不是处处可导的,但是我们
可以利用函数subgradient(局部可导)的性质,来优化这个函数。
W的搜寻是属于一个优化问题,由于我们后面介绍的神经网络的loss function并不是凸函数,虽然我们现在看到的SVM loss function是一个凸函数,但是我们并不打算
直接用凸优化的相关方法来找这个W,我们要介绍一种在后面的神经网络也能用到的优化技术来优化这个SVM loss function。
方案一:随机搜索
最简单,但是最糟糕的方案就是随机搜索,我们对W赋予一系列的随机值,然后看哪个随机值对应的loss最低,这样肯定是耗时而且低效的。
方案二:随机局部搜索
在随机搜索的基础上,加上一个局部搜索,即W+σW,我们会判断这个更新是有助于loss减小还是增大,如果是减小,那么我们就更新,反之就不更新,而继续做
局部搜索。
方案三:梯度下降
最简洁高效的算法就是梯度下降法,这种方法也是神经网络优化方法中用的最多的一种方法。
一般来说,我们会Back-propagation去计算loss function对W的偏导数, 这是利用链式法则(chain-rule)来计算梯度的一种方式.
声明:lecture notes里的图片都来源于该课程的网站,只能用于学习,请勿作其它用途,如需转载,请说明该课程为引用来源。课程网站: http://cs231n.stanford.edu/

