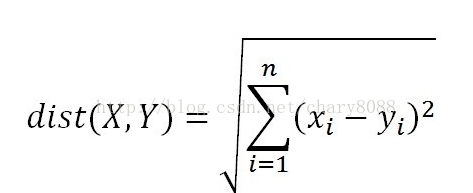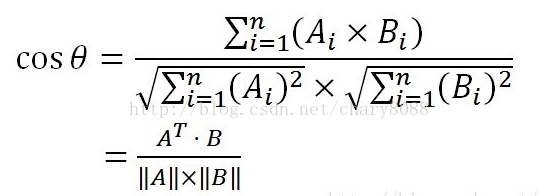来自:http://www.mtcnn.com
>>> import numpy
>>> vec1=[[1,1,1],[2,2,2]]
>>> vec2=[[2,2,2],[1,1,1]]
>>> vec1=numpy.array(vec1)
>>> vec2=numpy.array(vec2)
>>> vec1
array([[1, 1, 1],
[2, 2, 2]])
>>> vec2
array([[2, 2, 2],
[1, 1, 1]])
>>> dist = numpy.sqrt(numpy.sum(numpy.square(vec1 - vec2)))
>>> dist
2.4494897427831779
>>> numpy.linalg.norm(vec1-vec2)
2.4494897427831779余弦相似度:
>>> vec1
array([[1, 1, 1],
[2, 2, 2]])
>>> vec2
array([[2, 2, 2],
[1, 1, 1]])
>>> num=float(numpy.sum(vec1*vec2))
>>> num
12.0
>>> denom=numpy.linalg.norm(vec1)*numpy.linalg.norm(vec2)
>>> cos=num/denom
>>> denom
15.000000000000002
>>> cos
0.79999999999999993
>>> sim=0.5+0.5*cos
>>> sim
0.89999999999999991
两者相同的地方,就是在机器学习中都可以用来计算相似度,但是两者的含义有很大差别,以我的理解就是:
前者是看成坐标系中两个 点 ,来计算两点之间的 距离 ;
后者是看成坐标系中两个 向量 ,来计算两向量之间的 夹角 。
前者因为是 点 ,所以一般指 位置 上的差别,即 距离 ;
后者因为是 向量 ,所以一般指 方向 上的差别,即所成 夹角 。
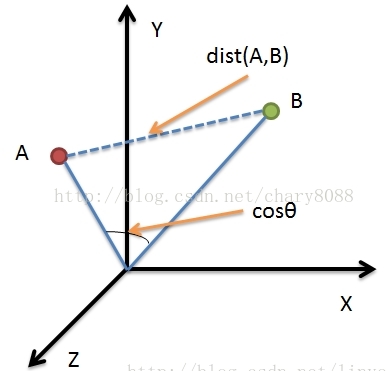
如下图所示:
数据项A和B在坐标图中当做点时,两者相似度为距离dist(A,B),可通过欧氏距离(也叫欧几里得距离)公式计算:
当做向量时,两者相似度为cosθ,可通过余弦公式计算:
假设||A||、||B||表示向量A、B的2范数,例如向量[1,2,3]的2范数为:
√(1²+2²+3²) = √14
numpy中提供了范数的计算工具: linalg.norm()
所以计算cosθ起来非常方便(假定A、B均为列向量):
num = float(A.T * B) #若为行向量则 A * B.T
denom = linalg.norm(A) * linalg.norm(B)
cos = num / denom #余弦值
sim = 0.5 + 0.5 * cos #归一化因为有了linalg.norm(),欧氏距离公式实现起来更为方便:
dist = linalg.norm(A - B)
sim = 1.0 / (1.0 + dist) #归一化关于归一化:
因为余弦值的范围是 [-1,+1] ,相似度计算时一般需要把值归一化到 [0,1],一般通过如下方式:
sim = 0.5 + 0.5 * cosθ
若在欧氏距离公式中,取值范围会很大,一般通过如下方式归一化:
sim = 1 / (1 + dist ( X,Y ))
说完了原理,简单扯下实际意义,举个栗子吧:
例如某T恤从100块降到了50块(A(100,50)),某西装从1000块降到了500块(B(1000,500))
那么T恤和西装都是降价了50%,两者的价格变动趋势一致,余弦相似度为最大值,即两者有很高的 变化趋势相似度
但是从商品价格本身的角度来说,两者相差了好几百块的差距,欧氏距离较大,即两者有较低的 价格相似度