四、线性美学
在 javascript动画、运动算法详细解释与分析 (一、Tween 运动算法) 中我们简单介绍了一下线性动画在javascript中的实现,你可能会像刚开始的我一样感觉这个动画直白,生硬,不自然,没有任何趣味性。而我们现实生活中也不会存在这样的匀速,直线,从0px移动到300px的灰色箱子。。但想象一下,如果我们的箱子会缓动,会弹跳,会变形,那就会有意思的多。
现实生活中,物体的运动都存在加速度或者缓冲,物体不可能从一个速度突然蹦到另外一个速度。如果我们用符合自然现实的方式实现我们的动画,那么我们的动画看起来才会更加自然、生动、流畅。那么现在,我们就来看一下“缓动”。
五、各种缓动
缓入缓出曲线:
|
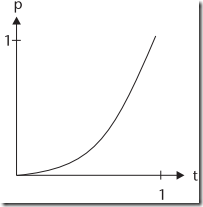
缓入:起始速度很慢,然后开始加速度。运动曲线(此时,斜率从0开始,并逐渐向1靠近) |
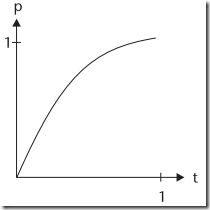
缓出:起始速度很快,然后减速,直到速度为0。运动曲线(斜率从1开始,逐渐向0靠近) |
缓入缓出:这个运动演示了物体运动从开始到结束的全过程(斜率从0到1,再从1到0) |
 |
 |
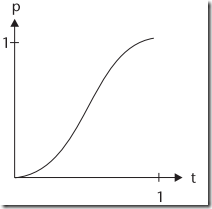 |
下面我们具体的看一下各种缓动曲线及公式:
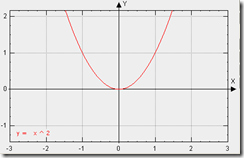
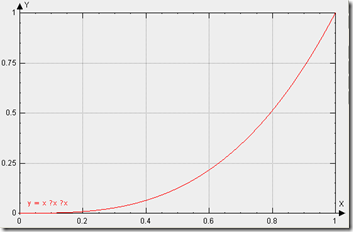
缓动类型:二次缓动
曲线类型:实际上就是二次方曲线(抛物线),p(t) = t ^ 2
曲线图示:
动画函数:
1: p = function( t, b, c, d){
2: return (t/=d)*t*c + b;
3: }
javascript实例:
1: /* des:tween算法。
2: t: 动画已经执行的时间(实际上时执行多少次/帧数)
3: b: 起始位置
4: c: 终止位置
5: d: 从起始位置到终止位置的经过时间(实际上时执行多少次/帧数)*/
6: tween = {
7: quad : function( t, b, c, d){
8: return (t/=d)*t*c + b;
9: }
10: }
虽然我们不是搞数学的,不过这里还是有必要解释一下这个公式,这里和我们之前的直线算法(p = t/d*c+b)一样,也是以t为变量,求p,只不过这里计算的是变量的平方。直线算法中,t*c/d+b表示当前事件量乘以不变的速度(c/d)再加上起始位置。但缓入算法中因为每时间片内的速度不一致,所以不能直接用c/d,既然是二次方抛物线,可能有同学就会想,那我直接写成p = t * t /d * c + b不就行了么,恩,你猜对了,这确实是一个二次方抛物线,不过,如果你尝试一下,你就会发现,这个抛物线会直接把物体抛到一个非常神秘非常遥远的地方。实际上我们这里的抛物线是有限制的,什么限制呢,0 <= p <= c,0 <= t <= d。整理该公式:
0 <= p <= c
0 <= t * c / d + b <= c
//b为常数,我们假设起始位置为0,得
0 <= t * c / d <= c
//两边处以c,得
0 <= t / d <= 1
这时候,公式从p = f(t)变成了p = f(t^2),也就是说0 <= p <=c,0 <= t^2 <= d。那么我们得到:
0 <= (t/d)^2 <= 1
这时其实我们已经可以看到,t与d的斜率为1,匀速运动;斜率从0到1变化,缓入运动;从1到0变化,缓出运动。缓入缓出运动实际上就是两者结合,时间各为二分之一。下面给出二次方曲线算法,并解释。
1: Quad: {
2: //缓入函数:斜率从0到1。
3: easeIn: function(t,b,c,d){
4: return c*(t/=d)*t + b;
5: },
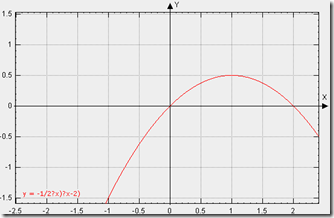
6: //缓出函数:将c系数变为负值使图形翻转,然后对t减2,使图形向右平移至正确位置
7: easeOut: function(t,b,c,d){
8: return -c *(t/=d)*(t-2) + b;
9: },
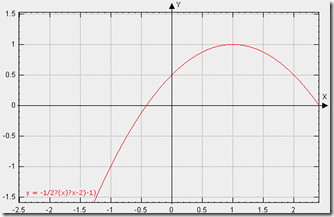
10: //缓入缓出
11: easeInOut: function(t,b,c,d){
12: //判断当前时间是否在总时间的一半以内,是的话执行缓入函数,否则的话执行缓出函数
13: if ((t/=d/2) < 1) return c/2*t*t + b;
14: //将总长度设置为一半,并且时间从当前开始递减,对图像进行垂直向上平移。公式变形过程如下图
15: return -c/2 * ((--t)*(t-2) - 1) + b;
16: }
17: }
下面我们就可以引用这些算法来实现简单的缓动效果了。我们使用在《javascript动画、运动算法详细解释与分析一》中的move.startMove("movingBox","quadEasyInOut",null,null,600);来实现我们的二次方缓动效果。那么你将会看到一块儿板砖努力的从左边移动到右边然后再使劲儿的停下来。
下面我们一起来看一下三次方,四次方以及五次方曲线运动,因为大体思路都是一致的,只不过运动速度(也就是函数曲线斜率变化更快了一点而已)。所以这里只解释算法以及图形变化。
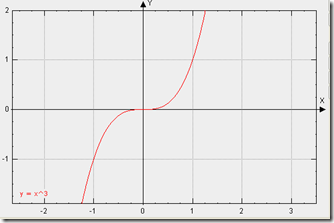
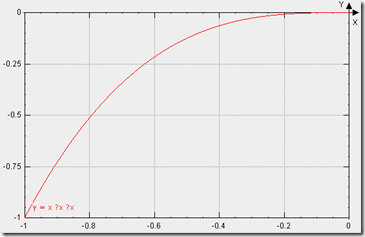
缓动类型:三次方缓动
曲线类型:实际上就是三次方曲线(抛物线),p(t) = t ^ 3
曲线图示:基本图形
运动函数:
1: Cubic: {
2: //缓入:t/=d,使t的取值始终在 0 至 1 之间,c作为系数来改变返回值的范围(路程的长度范围),图形如下
3: easeIn: function(t,b,c,d){
4: return c*(t/=d)*t*t + b;
5: },
6: //缓出:t=t/d-1,使t的取值在 -1 至 0 之间,此时图形如下
7: easeOut: function(t,b,c,d){
8: return c*((t=t/d-1)*t*t + 1) + b;
9: },
10: //缓入缓出:
11: easeInOut: function(t,b,c,d){
12: // t/=d/2 < 1,缓入,当前时间除以总时间的一半之后如果小于1(当前时间小于总时间的一半,只不过这里可以比较并且赋值,此时0 < t < 2),图略
13: if ((t/=d/2) < 1) return c/2*t*t*t + b;
14: //否则,缓出,此时t值从-1向0过度(t-=2的作用仅仅在于将t的取值范围控制在-1至0之间),图略。貌似算法和上面两种分开来的算法不一样,
实际上只是t的取值根据上下文的环境发生了改变而已,图像还是一样的,只不过后一半路程的起始和终止点的范围需要改变一下。
15: return c/2*((t-=2)*t*t + 2) + b;
16: }
17: }
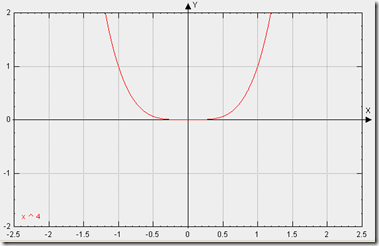
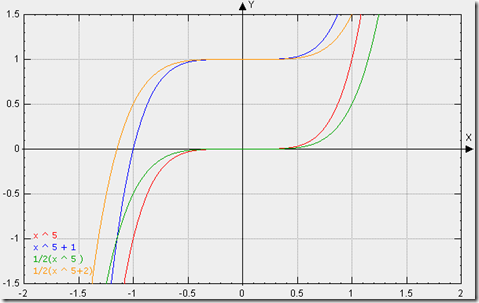
缓动类型:四次方缓动
曲线类型:四次方曲线(抛物线),p(t) = t ^ 4
曲线图示:基本图形
运动函数:
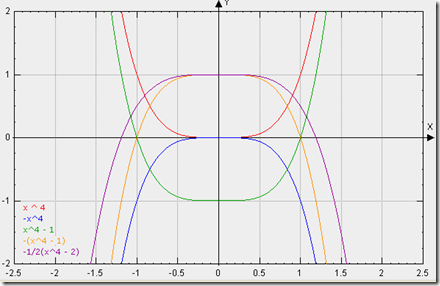
1: //四次方曲线,各个函数图像变化如下图,你可以根据函数公式和x取值范围来推断函数曲线在y轴上的取值范围
2: /*基本演变公式:
3: x ^ 4;
4: -x^4;
5: x^4 - 1;
6: -(x^4 - 1);
7: -1/2(x^4 - 2);*/
8: Quart: {
9: //缓入:t取值在0至1之间,
10: easeIn: function(t,b,c,d){
11: return c*(t/=d)*t*t*t + b;
12: },
13: //缓出:t取值在-1至0之间,因子数-1,图像向上平移1个单位,系数为负数,垂直翻转图像。
14: easeOut: function(t,b,c,d){
15: return -c * ((t=t/d-1)*t*t*t - 1) + b;
16: },
17: //缓入缓出:
18: easeInOut: function(t,b,c,d){
19: //如果当前时间除以总时间的一半之后小于1。因为起始位置是0,所以直接可以使用缓入公式。
20: if ((t/=d/2) < 1) return c/2*t*t*t*t + b;
21: //但若当前时间大于总时间的一半,那么使t=t-2,t取值在(-1至0)之间,通过因子数-2使图像向上平移2个单位,此时函数值在1至2之间,但c/2使函数值
得取值范围变为0.5至1,这样函数值的初值就变为总路程的一半,并且终值依然为1。
22: return -c/2 * ((t-=2)*t*t*t - 2) + b;
23: }
24: }
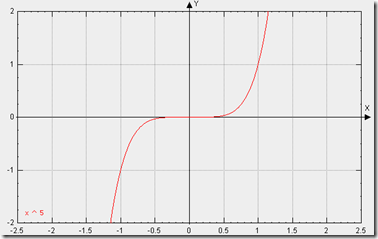
缓动类型:五次方缓动
曲线类型:四次方曲线(抛物线),p(t) = t ^ 5
曲线图示:基本图形
运动函数:
1: //5次方曲线,只给出图像,公式不再解释,都一个娘生的。
//稍微解释下吧。红色线是缓入图像x取值范围[0,1]。蓝色线是缓出图像,x取值范围[-1,0]。绿色线是缓入缓出中的前一半缓入图像,x取值范围[0,1]。黄色线为缓入缓出中的后一半缓入图像,x取值范围[-1,0]。
2: Quint: {
3: easeIn: function(t,b,c,d){
4: return c*(t/=d)*t*t*t*t + b;
5: },
6: easeOut: function(t,b,c,d){
7: return c*((t=t/d-1)*t*t*t*t + 1) + b;
8: },
9: easeInOut: function(t,b,c,d){
10: if ((t/=d/2) < 1) return c/2*t*t*t*t*t + b;
11: return c/2*((t-=2)*t*t*t*t + 2) + b;
12: }
13: }
OK。
到这里简单缓入缓出动画解析完毕,如果童鞋们有任何意见或者建议或者问题,都可以与本人联系。
本人在下一篇中将讨论一下稍微复杂一点的曲线运动。