POJ1269 Intersecting Lines

嘟嘟嘟
翻译：直线求交。


本人第一道计算几何题。已经体会到了计算几何的恶心之处……

首先当然有联立解析式的做法，然而在咱竞赛中一般都用向量的求法。
然后刚开始我就因为怎么存向量和直线的事情折腾了好半天：刚开始开了一个向量类和一个直线类，但是发现这样封装过度了，就把直线类删了。但是单纯的开一个向量类又不够，就又开了一个结构体存单点。反正最后一个比较优美的写法就是开一个向量类和单点，然后单点的变量名都是单个大写字母，向量的变量名都是两个大写字母。比如两个点(A, B)，那么(overrightarrow{AB})就叫(AB)。


[说正事儿]
直线求交比线段求交要简单点，只用判断是否平行或共线即可。
对于两条直线(AB, CD)。平行的条件是(overrightarrow{AB} imes overrightarrow{CD} = 0)。在这个前提下再判断共线：(overrightarrow{AB} imes overrightarrow{AC} = 0)。如果这俩都不是，那么一定有交点。
下面具体讲讲怎么求交点。

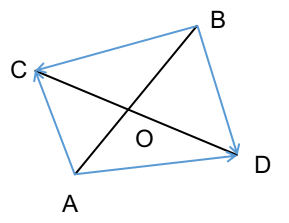
因为(A)点坐标已知，所以我们可以通过求出(overrightarrow{AB})以及(AO)和(AB)的比来得到(O)点坐标。
而(frac{AO}{AB} = frac{S_{Delta ACD}}{S_{Delta ACD} + S_{Delta BCD}})，且(S_{Delta ACD} = overrightarrow{AC} imes overrightarrow{AD})，(S_{Delta BCD} = overrightarrow{BC} imes overrightarrow{BD})。那么问题就迎刃而解了：(O = A + frac{overrightarrow{AB} imes S_{Delta ACD}}{S_{Delta ACD} + S_{Delta BCD}})。


代码还是相当清真的

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
//const int maxn = ;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n;
struct Vec
{
  int x, y;
  friend Vec mul(const Vec& A, const int& k)
  {
    return (Vec){A.x * k, A.y * k};
  }
  int operator * (const Vec& oth)const
  {
    return x * oth.y - oth.x * y;
  }
  int dot (const Vec& oth)const
  {
    return x * oth.x + y * oth.y;
  }
};
struct Point
{
  int x, y;
  Vec operator - (const Point& oth)const
  {
    return (Vec){x - oth.x, y - oth.y};
  }
}A, B, C, D;

void solve()
{
  Vec AB = B - A, CD = D - C;
  if(AB * CD == 0)
    {
      Vec AC = C - A;
      if(AB * AC == 0) puts("LINE");
      else puts("NONE");
      return;
    }
  Vec AC = C - A, AD = D - A, BD = D - B, BC = C - B;
  int s1 = AC * AD, s2 = BD * BC;
  Vec _AB = mul(AB, s1);
  db x = (db)_AB.x / (db)(s1 + s2), y = (db)_AB.y / (db)(s1 + s2);
  printf("POINT %.2lf %.2lf
", (db)A.x + x, (db)A.y + y);
}

int main()
{
  puts("INTERSECTING LINES OUTPUT");
  n = read();
  for(int i = 1; i <= n; ++i)
    {
      A.x = read(); A.y = read(); B.x = read(); B.y = read();
      C.x = read(); C.y = read(); D.x = read(); D.y = read();
      solve();
    }
  puts("END OF OUTPUT");
  return 0;
}