很显然是一道最小割模型。
做完几道题后。图的大概就能想出来了:
1.对于每一个动物,如果是0,就和s连一条边,否则向t连一条边。
2.对于每一个任务,题中要求最大利润,可以转化成最小损失。
(1)如果都要变成1,就向汇点连一条w +g(如果有的话)的边;否则从源点连一条w +g的边。接下来
(2)对于任务中涉及的每一个点,刚开始我想如果任务要变成1,而他本身还是1就不连边,否则连一条INF的边,然后我就发现任务之间是互相影响的,而这种方式体现不出来,然后我就想不出来了……
题解是这么说的:如果这个任务是0,就向所有涉及到的点连边,否则这些点向他连边,然后我就画了一个图,发现好像还真是这么回事:
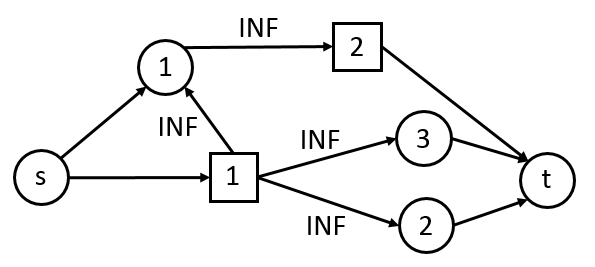
如果我们要达成任务1的话,就要割掉(2->t), (3->t)两条边,但是图还是联通的,因此还得割掉([2]->t)的边,也就同时说明了任务2不可达成。

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<cstdlib> 7 #include<cctype> 8 #include<vector> 9 #include<stack> 10 #include<queue> 11 using namespace std; 12 #define enter puts("") 13 #define space putchar(' ') 14 #define Mem(a, x) memset(a, x, sizeof(a)) 15 #define rg register 16 typedef long long ll; 17 typedef double db; 18 const int INF = 0x3f3f3f3f; 19 const db eps = 1e-8; 20 const int maxn = 1.2e4 + 5; 21 inline ll read() 22 { 23 ll ans = 0; 24 char ch = getchar(), last = ' '; 25 while(!isdigit(ch)) {last = ch; ch = getchar();} 26 while(isdigit(ch)) {ans = ans * 10 + ch - '0'; ch = getchar();} 27 if(last == '-') ans = -ans; 28 return ans; 29 } 30 inline void write(ll x) 31 { 32 if(x < 0) x = -x, putchar('-'); 33 if(x >= 10) write(x / 10); 34 putchar(x % 10 + '0'); 35 } 36 37 int n, m, t; 38 int g, val[maxn], sum = 0; 39 bool a[maxn]; 40 41 struct Edge 42 { 43 int from, to, cap, flow; 44 }; 45 vector<Edge> edges; 46 vector<int> G[maxn]; 47 void addEdge(int from, int to, int w) 48 { 49 edges.push_back((Edge){from, to, w, 0}); 50 edges.push_back((Edge){to, from, 0, 0}); 51 int sz = edges.size(); 52 G[from].push_back(sz - 2); 53 G[to].push_back(sz - 1); 54 } 55 56 int dis[maxn]; 57 bool bfs() 58 { 59 Mem(dis, 0); dis[0] = 1; 60 queue<int> q; q.push(0); 61 while(!q.empty()) 62 { 63 int now = q.front(); q.pop(); 64 for(int i = 0; i < (int)G[now].size(); ++i) 65 { 66 Edge& e = edges[G[now][i]]; 67 if(!dis[e.to] && e.cap > e.flow) 68 { 69 dis[e.to] = dis[now] + 1; 70 q.push(e.to); 71 } 72 } 73 } 74 return dis[t]; 75 } 76 int cur[maxn]; 77 int dfs(int now, int res) 78 { 79 if(now == t || res == 0) return res; 80 int flow = 0, f; 81 for(int& i = cur[now]; i < (int)G[now].size(); ++i) 82 { 83 Edge& e = edges[G[now][i]]; 84 if(dis[e.to] == dis[now] + 1 && (f = dfs(e.to, min(res, e.cap - e.flow))) > 0) 85 { 86 e.flow += f; 87 edges[G[now][i] ^ 1].flow -= f; 88 flow += f; res -= f; 89 if(res == 0) break; 90 } 91 } 92 return flow; 93 } 94 95 int minCut() 96 { 97 int flow = 0; 98 while(bfs()) 99 { 100 Mem(cur, 0); 101 flow += dfs(0, INF); 102 } 103 return flow; 104 } 105 106 int main() 107 { 108 n = read(), m = read(), g = read(); 109 t = n + m + 1; 110 for(int i = 1; i <= n; ++i) a[i] = (bool)read(); 111 for(int i = 1; i <= n; ++i) 112 { 113 int x = read(); 114 if(a[i]) addEdge(i, t, x); 115 else addEdge(0, i, x); 116 } 117 for(int i = 1; i <= m; ++i) 118 { 119 int op = read(), w = read(), k = read(); 120 sum += w; 121 for(int j = 1; j <= k; ++j) 122 { 123 int id = read(); 124 if(op) addEdge(id, i + n, INF); 125 else addEdge(i + n, id, INF); 126 } 127 int flg = read(); 128 if(op) addEdge(i + n, t, w + flg * g); 129 else addEdge(0, i + n, w + flg * g); 130 } 131 write(sum - minCut()); enter; 132 return 0; 133 }
