RMQ 即范围最小值问题 (Range Minimum Query)。给出一个 n 个元素的数组,设计一个数据结构,支持查询操作 Query(L, R):计算该区间内的最小值。
如果用朴素的算法的话,每一次一个循环求解,那时间复杂度就达到了 O(mn),显然不够快。在实践中,最常用的是 Tarjan 的 Sparse - Table(st 表)算法,主要功能是解决静态区间最值问题。它用 O(nlogn)预处理,而查询只用 O(1),且常数很小。
这个算法具体是这么写的:开一个二维数组 dp[i][j] ,表示从 i 开始的,长度为 2 ^ j 的一段元素的最小值,这样就可以用递推的方法计算 dp[i][j] : dp[i][j] = min(dp[i][j - 1], dp[i + 2 ^ (j - 1)][j - 1])。原理如下图所示:
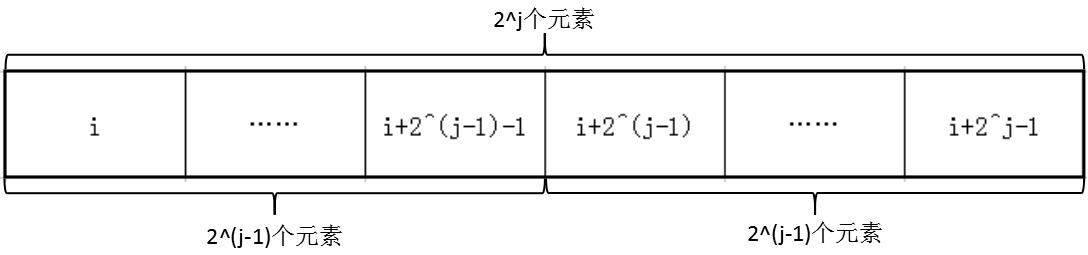
可以看出,这是利用归并的思想。
因为2^j <= n,因此dp数组的元素个数不超过 nlogn 个,而且每一项都可以在常数时间计算完毕,所以时间复杂度为 O(nlogn)。上代码
1 void RMQ_init() 2 { 3 for(int i = 1; i <= n; ++i) dp[i][0] = a[i]; //此时长度为1,个只有一个元素。 4 for(int j = 1; (1 << j) <= n; ++j) 5 /*长度一定要放在外层循环,这样才能保证每一个元素都被更新到 , 6 跟区间dp原理一样*/ 7 for(int i = 1; i + (1 << j) - 1 <= n; ++i) 8 { 9 dp[i][j] = min(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]); 10 } 11 }
查询也很简单,令 k 满足 2 ^ k <= R - L + 1 的最大整数,则以 L 开头,R 结尾的两个长度为2 ^ k 的区间合起来就覆盖了要查询的区间 [L, R]。由于是取最小值,因此两个子区间有重叠的部分也没关系,代码如下
1 int query(int L, int R) 2 { 3 int k = 0; 4 while(1 << (k + 1) <= R - L + 1) k++; 5 //注意是 k + 1,而不是k,因为这么写的话,符合条件k还要再+1,就应返回dp[L][k - 1]了 6 return min(dp[L][k], dp[R - (1 << k) + 1][k]); 7 }
不过这样查询的时间复杂度就是 O(logn)。只要初始化 k,开一个数组 que[i],代表长度为 i 时 k 的取值,查询的复杂度就能达到 O(1)了。
int k = 0; for(int i = 1; i <= n; ++i) { if ((1 << k) <= i) k++; que[i] = k - 1; } void query(int L, int R) { int k = que[R - L + 1]; return min(dp[L][k], dp[R - (1 << k) + 1][k]); }