【问题描述】
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:n 个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师再次吹哨子时,传球停止,此时,拿着球没传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了m 次以后,又回到小蛮手里。两种传球的方法被视作不同的方法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有3 个同学1 号、2 号、3号,并假设小蛮为1 号,球传了3 次回到小蛮手里的方式有1->2->3->1 和1->3->2->1,共2种。
【输入】
输入文件ball.in 共一行,有两个用空格隔开的整数n,m(3<=n<=30,1<=m<=30)。
【输出】
输出文件ball.out 共一行,有一个整数,表示符合题意的方法数。
【输入输出样例】
ball.in ball.out
3 3 2
【限制】
40%的数据满足:3<=n<=30,1<=m<=20
100%的数据满足:3<=n<=30,1<=m<=30
这道题与其说是递推题,更不如说是dp题。想这道题时要用一种“状态转化”的思维。
根据题意,咱们先任取一个位置i,那么他只能从左面i - 1,或右面i + 1传过来。所以传到i的方案数就等于i - 1加上i + 1的方案数(加法原理)。
设dp[i][j]表示传了i次球到j位置的方案数,那么dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
上代码:
1 #include<cstdio>
2 #include<iostream>
3 #include<cstring>
4 #include<cmath>
5 #include<algorithm>
6 typedef long long ll;
7 int n ,m;
8 ll f[35][35];
9 int main()
10 {
11 freopen("ball1.in", "r", stdin);
12 freopen("ball1.out", "w", stdout);
13 scanf("%d%d", &n, &m); //n人,m次
14 f[0][0] = 1; //这种情况方案数1
15 for(int i = 1; i <= m; ++i)
16 {
17 for(int j = 0;j < n; ++j)
18 {
19 f[i][j] = f[i - 1][(j + n - 1) % n] + f[i - 1][(j + 1) % n];
20 }
21 }
22 printf("%lld\n", f[m][0]);
23 return 0;
24 }
注意:dp[i][j]表示传了i次球到j位置的方案数,而不是传了j次球到i位置的方案数。因为这样的话递推方程dp[i][j] = dp[i - 1][j - 1] + dp[i + 1][j - 1];更新i的时候i + 1还没有被更新过,所以dp[i + 1][j - 1]就是0,出错。
这么看来,外层循环的i大多数情况下都应该是严格单调的,这样才能保证更新i的时候,用来更新它的数组元素已经被更新过。
扩展:如果m规定<= 10 ^ 9 呢?
用上述朴实的算法时间肯定撑不住,那么就需要用矩阵乘法来优化了。
用矩乘,要先思考这么几步:一、状态是如何转移的。二、矩阵长什么样。
慢慢分析
一、状态是如何转移的
其实这一步应该是递推递归以及dp的思路,要不哪来的状态转移方程呢?
咱们再来回顾一下这个方程:dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1]; 可见 dp[i][j] 是从 dp[i - 1][j - 1] 和 dp[i - 1][j + 1]更新过来的,而 dp[i - 1][j - 1] 和 dp[i -1][j + 1] 又分别是从各自的两侧更新过来的。如此推广,dp[i][j] 似乎跟 dp[i 到 n][j 到 m] 都有关,所以
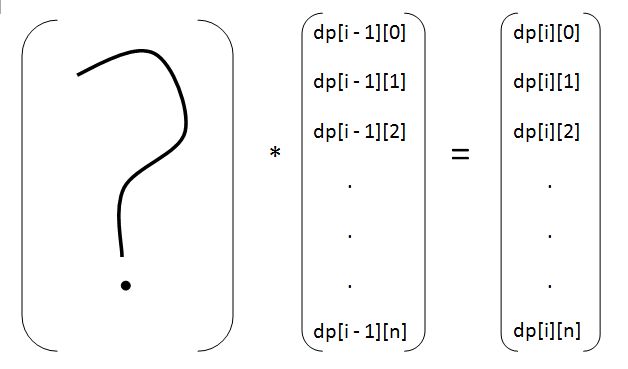
嗯第二步。
二、矩阵长什么样
这就不难想了。看上图找规律:dp[i][0] = dp[i - 1][n](因为是环嘛,0 - 1 就是 n) + dp[i - 1][1], dp[i][1] = dp[i - 1][0] + dp[i - 1][2], dp[i][2] = dp[i - 1][1] + dp[i - 1][3] ...... dp[i][n] = dp[i - 1][n - 1] + dp[i - 1][0]。所以矩阵就是这个样子了
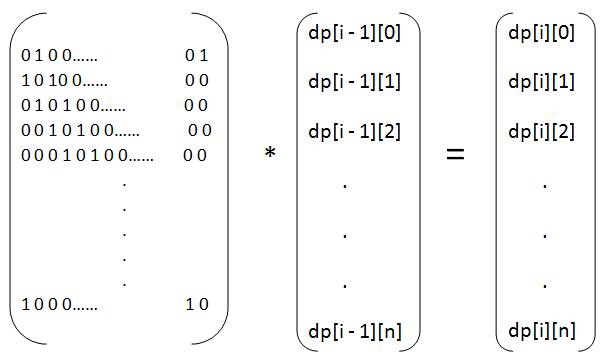
我觉得已经可以上代码了
1 #include<cstdio>
2 #include<cstring>
3 #include<algorithm>
4 #include<iostream>
5 using namespace std;
6 const int maxn = 35;
7 const int mod = 10000; //对10000取模
8 int n, m;
9 struct Mat{
10 int a[maxn][maxn];
11 Mat operator * (const Mat& other)const{ //改一下乘号,使两个矩阵能相乘
12 Mat ans; memset(ans.a, 0, sizeof(ans.a));
13 for(int i = 0; i < n; ++i)
14 for(int j = 0; j < n; ++j)
15 for(int k = 0; k < n; ++k)
16 {
17 ans.a[i][j] += a[i][k] * other.a[k][j];
18 ans.a[i][j] %= mod;
19 }
20 return ans;
21 }
22 };
23 Mat quickpow(Mat A, int num)
24 {
25 Mat ret; memset(ret.a, 0, sizeof(ret.a));
26 for(int i = 0; i < n; ++i) ret.a[i][i] = 1;
27 while(num)
28 {
29 if(num % 2 == 1) ret = ret * A;
30 A = A * A;
31 num >>= 1;
32 }
33 return ret;
34 }
35 void init(Mat &X) //初始化矩阵
36 {
37 memset(X.a, 0, sizeof(X.a));
38 X.a[0][1] = 1;X.a[0][n - 1] = 1; //第一行和最后一行手动初始化
39 X.a[n - 1][0] = 1;X.a[n - 1][n - 2] = 1;
40 for(int i = 1; i < n - 1; ++i) //中间的用for循环初始化
41 {
42 X.a[i][i - 1] = X.a[i][i + 1] = 1;
43 }
44 return;
45 }
46 int main()
47 {
48 scanf("%d%d", &n ,&m);
49 Mat A;
50 init(A);
51 Mat B = quickpow(A, m);
52 int ans = B.a[0][0];
53 printf("%d\n", ans);
54 return 0;
55 }
收尾。