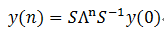行列式三个作用
1. 求逆用得到
2. 求线性方程组用得到
3. 求特征值和特征向量用得到
4. 求平行六面体的体积和平行四边形的面积
其中我认为要数第三个最有意义。因为高阶微分方程或一阶多变量方程组可以通过简单的转化,都变成一阶单变量微分方程!!也就是变成如下简单的形式
dy/dt=Ay
其中y是向量形式的变量,A是方阵,设其为n*n。它的解为:
<img src="https://pic2.zhimg.com/50/376de4d68a39576197d8910f57d681c1_hd.jpg" data-rawwidth="169" data-rawheight="37" class="content_image" width="169">
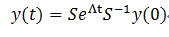
其中S的每列为A的n个特征向量,Λ为A对角化之后的方阵,它的对角线为A的n个特征值。
是不是相当简单!!
对于差分方程也同样道理,高阶的和多变量的,最终化成如下形式
y(n+1)=Ay(n)
其中y(n+1)和y(n)是向量形式的变量,A是方阵,设其为n*n。它的解为:
<img src="https://pic1.zhimg.com/50/c3e0c23afe257acb5951f085278e223e_hd.jpg" data-rawwidth="164" data-rawheight="34" class="content_image" width="164">
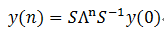
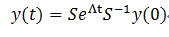 其中S的每列为A的n个特征向量,Λ为A对角化之后的方阵,它的对角线为A的n个特征值。
其中S的每列为A的n个特征向量,Λ为A对角化之后的方阵,它的对角线为A的n个特征值。