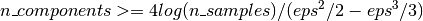Johnson–Lindenstrauss 定理是这样的:一个一百万维空间里的随便一万个点,一定可以几乎被装进一个几十维的子空间里!
严格说来是这样:在 M 维空间中的 N 个点,几乎总是被包含在一个 D 维子空间里的。这里的 D 按照直觉应当等于 N 的阶,可是实际上我们只需要让 D 是 log(N) 的阶就可以了。这里「几乎被包含在」的确切含义是它在这个子空间上的投影几乎是等距的(允许有一个 ε 的误差,而常数 D/log(N) 就依赖于 ε)。很显然,这件事情在高维数据降维时有极重要的意义。
这个定理的证明很初等。它依赖于这样的一个基本概率事实:一个随机的 M 维单位向量到一个随机的 D 维子空间上的投影的长度几乎一定约等于 D/M。这件事情本身也有点不同寻常,虽然它可以通过简单的计算来证实。这是概率论计算中常常出现的由于高维度而导致的反直觉现象的一例。
这让我想起另一个高维度导致的悖论,是我在学大数定律时了解到的。在 M 维单位立方体中随机取一个点,当 M 充分大时根据大数定理容易算出这个点到立方体中心的距离几乎一定等于 √(M/3)/2。于是这就说明 M 维实心单位立方体几乎就完全位于一个半径为 √(M/3)/2 的球壳上。这里没有任何捣鬼之处,事实上就是如此。
Johnson–Lindenstrauss 引理表明任何高维数据集均可以被随机投影到一个较低维度的欧氏空间,同时可以控制pairwise距离的失真.
理论边界
由一个随机投影P所引入的失真是确定的,这是由于p定义了一个esp-embedding.其概率论定义如下:

u和v是从一个形状是[n样例,n特征]=[n_samples, n_features]的数据集中的任意行,p室友一个形状是[n成分,n特征]=[n_components, n_features]的随机高斯N(0,1)矩阵的投影(或一个稀疏Achlioptas矩阵).
用于保证eps-embedding的最小成分数有下面的公式得到: