1.本周学习总结(0--2分)
1.思维导图
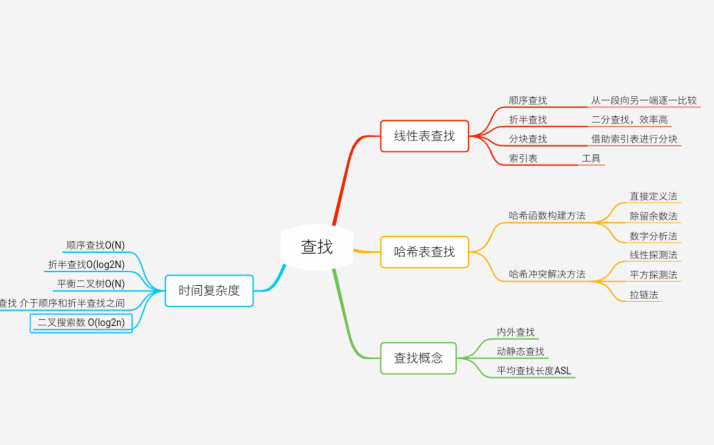
2.谈谈你对查找运算的认识及学习体会。
本章学习的是关于查找的有关知识,有线性表的查找:顺序查找、折半查找、索引储存结构和分块查找 树表查找:二叉排序树、平衡二叉树 B+- 树 红黑树 还有
哈希查找。 每种查找方法都有他可利用的价值和不同的特点。折半查找、二分查找:这个需要查找对象是有序的,每一次都找1/2的部分,查找次数大大的减少了。时间复杂度是O(logN)。二叉查找树的插入和删除都非常的方便,很好的解决了折半查找添加删除所带来的问题。平衡二叉树会解决二叉树在某种情况下会存在效率问题。B-的特点:
1.树中每个结点最多有 m 个孩子;
2、除根结点和叶子节点外,其他每个节点至少有 m / 2 个孩子;
3、若根结点不是叶子节点,则至少有 2 个孩子;
4、所有叶子结点都出现在同一层,叶子结点不包含任何关键字信息
其他算法就不一一介绍了,他们都各有各自的优点缺点,他们之间可以互补等等 通过学习本章的查找算法,我学到很多以前不知道的查找方法,了解到更多解决问题的好算法。
2.PTA实验作业(6分)
2.1.题目1:题目名称
是否二叉搜索树
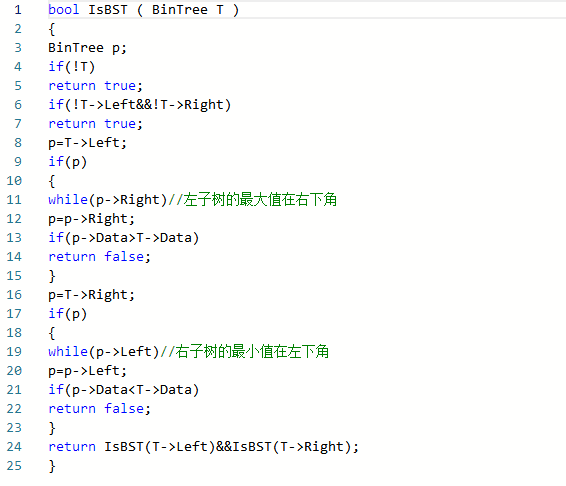
2.1.1设计思路(伪代码)
begin:
IsBST函数传入二叉树T
定义静态整型变量s=-1
定义bool类型变量result
if T为空 then 返回true end if
递归遍历左孩子,result接收返回值
if result为false 返回 false end if
else if T->Data大于s then s=T->Data end else if
else 返回false end else
递归遍历右孩子,result接收返回值
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
2.1.3本题PTA提交列表说明。

说明: A1.这道题代码量较少,所以在dvc打测试没什么问题,提交一遍过
2.2 题目2
7-1 QQ帐户的申请与登陆
2.2.1设计思路
int main()
{
输出数据
for (i = 0 to T)
{
输入数据
cin >> order >> account >> password;
if (order == 'N')
{
调用注册函数Register(account, password);
}
else
{
调用登录函数Login(account, password);
}
}
return 0;
}
void Register(string &account, string &password)
{
if(已经注册)
cout << "ERROR: Exist
";
else(没有注册)
mymap[account] = password;
cout << "New: OK
";
}
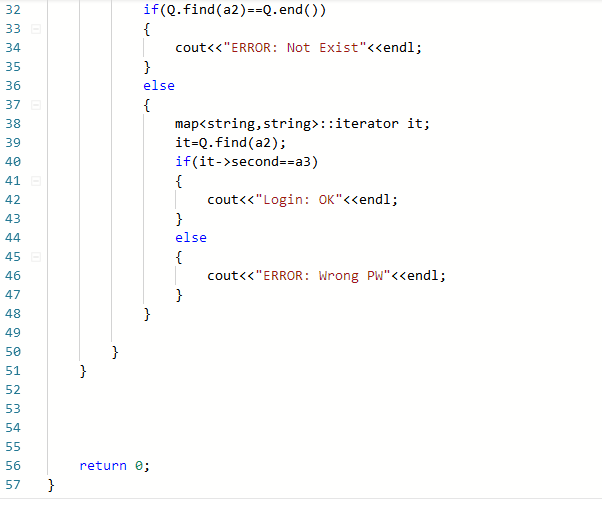
void Login(string &account, string &password)
{
if (账号不存在)
{
cout << "ERROR: Not Exist
";
}
else if(密码正确)
{
cout << "Login: OK
";
}
else 密码错误
{
cout << "ERROR: Wrong PW
";
}
}
2.2.2代码截图

2.2.3提交列表及说明
说明:Q1.在函数结束的地方没有return 0导致编译错误
A1.函数大部分用到c中的if else 语法,较易理解
2.3 题目3
7-2 航空公司VIP客户查询
2.3.1设计思路
begin:
定义n,遍历查找是否为会员
scanf("%d", &n);
while(n--) {
char c = '0';
scanf("%lld%c", &id, &c);
if(c == 'x') {
id = -id;
}
if(table.count(id)) {
printf("%lld
", table[id]);
} else {
printf("No Info
");
}
}
return 0;
}
2.3.2代码截图
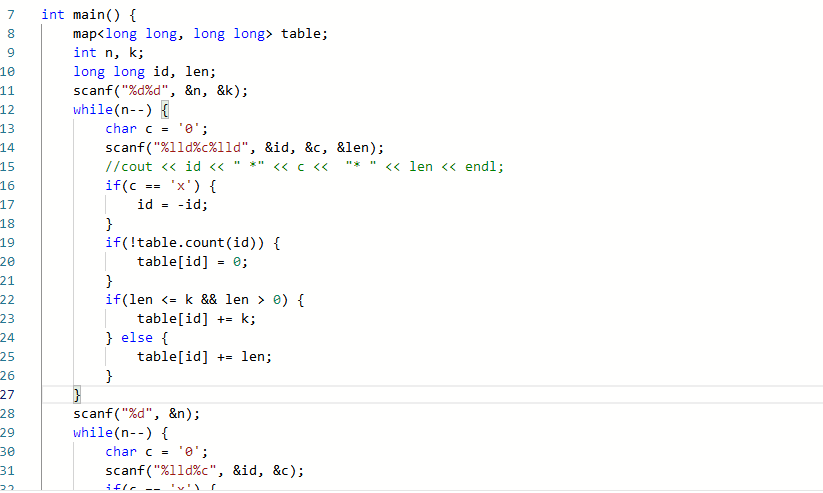
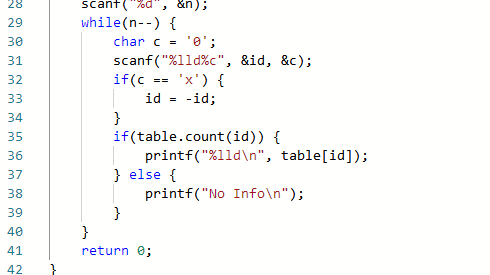
2.3.3提交列表及说明
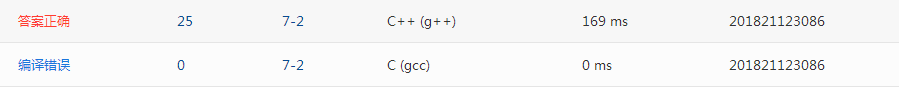
Q1.这题有些地方是参考同学思路的,循环遍历哪里修改了一下
Q2.编译错误: 用错了编译器
A1.从同学代码中了解到了新的查找思路
3、阅读代码(-2--2分)
找一份和查找运算相关代码,谈谈你对这个代码认识体会。
https://blog.csdn.net/xiezhi123456/article/details/87095823
设计程序,实现哈希表的相关运算,并完成如下功能:
* 1、建立关键字序列(16, 74, 60, 43, 54, 90, 46, 31, 29, 88, 77)对应的哈希
* 表A[0..12],哈希函数为H(k)=k%p,并采用开放地址法中的线性探测法解决冲突
*
* 这里的哈希表A[0..12],m=13,取p=m=13,哈希函数H(k)=k%13
* 解决冲突的线性探测法是:d(0)=H(k),d(i+1)=(d(i)+1)%m
* 2、在上述哈希表中查找关键字为29的记录
* 3、在上述哈希表中删除关键字为77的记录,再将其插入
体会: 通过阅读作者的哈希表的运算算法,我领会哈希表的构造和查找过程及其相关算法设计
作者的代码中有出现用循环结构处理哈希表中的冲突问题,算法中adr = (adr + 1) % m 采用线性探测法找下一个地址
我觉得是我学到并且认为很妙的一点。当然代码中还有比较多可以借鉴和学习的地方,总之收获还是非常大的