树 作业

1.本周学习总结

1.思维导图

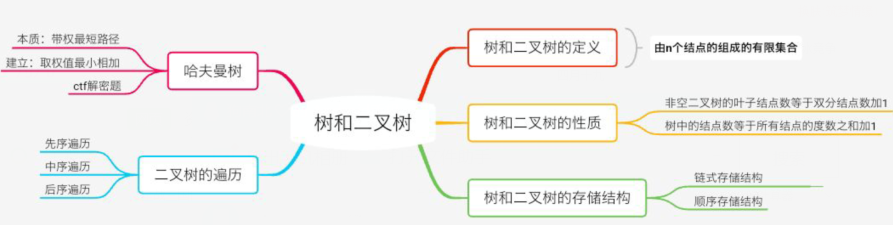
2.谈谈你对树结构的认识及学习体会。

树这一章主要学习了树的基本结构，有二叉树，满二叉树，完全二叉树的结构，对于二叉树又有三种不同的遍历方法1：先序遍历：根->左子树->右子树（先序）

2：中序遍历：左子树->根->右子树（中序）

3：后序遍历：左子树->右子树->根（后序）
学习树的结构又开启了新的代码的新世界

2.PTA实验作业

2.1.题目1：题目名称

6-3 求二叉树高度

2.1.1设计思路（伪代码）

int GetHeight( BinTree BT )
{
int m,n;
	if(BT==NULL) return 0;
	m=GetHeight(BT->Left);
	n=GetHeight(BT->Right);// 定义右孩子，左孩子。
根据树高度公式定义返回分支的 树高度
}```

#2.1.2代码截图
![](https://img2018.cnblogs.com/blog/1477754/201905/1477754-20190519113051613-809881142.png)

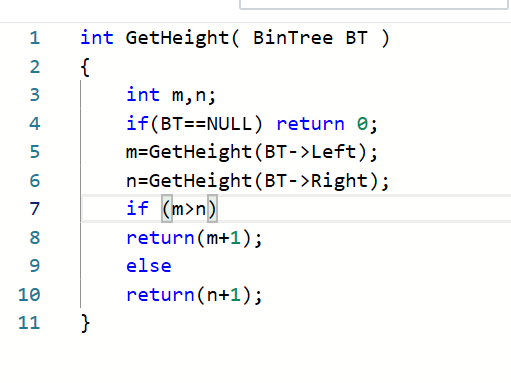
#2.1.3本题PTA提交列表说明。
![](https://img2018.cnblogs.com/blog/1477754/201905/1477754-20190519113143120-703592090.png)
说明:这道函数题，答案非常简单，相对较容易，思路较清晰  主要是在返回的那里要花一些时间去想和做简单口算
#题目2  2.2.1
7-4 jmu-ds-二叉树叶子结点带权路径长度和
##2.2.2

```begin：
void CreatTree(TNode * &t,int i,string str);
int put(TNode *t,int i);
void puut(TNode *t);
int main()
{
	int a;
	string str;
	getline(cin,str);
	TNode *t;
	CreatTree(t,1,str);
	a=put(t,0);
	cout<<a;
}//对于主函数的安排：先输入树的对应值，输出的是它的带权路径长度和
void CreatTree(TNode * &t,int i,string str)
{
        if(str[i]!='#')
		{
			当节点不为#时，输出该点的所应的值。
		}
		if(2*i<=str.length()-1) CreatTree(t->left,2*i,str);
	    if(2*i+1<=str.length()-1) CreatTree(t->right,2*i+1,str);
}
int put(TNode * t,int i)
{
	int j,x;
	if(t==NULL) return 0;//指空处理
	if(t->left==NULL&&t->right==NULL)
	{
		return i*(t->data-'0');
	}
	j=put(t->left,i+1);
	x=put(t->right,i+1);
    返回路径长度
}
void puut(TNode *t)
{
	if(t==NULL) cout<<'#';
	if(t!=NULL)
	{
		输出左孩子，右孩子各分支的长度
	}
}
end》》》

2.2.3

1.编译错误：函数入口定义的结构体错误
2.答案错误：算法出错，后来通过修改返回函数来得到正确答案

2.3 题目3

7-1 还原二叉树

2.3.1

begin:BTNode *CreatTree(char *pre,char *in,int n)
{
	定义指针，变量；
	if(n小于等于0)   返回空;
	b=new BTNode;//申请新的链接
	b->data=*pre;
	for(p=in;p<in+n;p++)
    {
	    if(指针所指和实际值相等) 退出循环;
	}
	k=p-in;
	b->left=CreatTree(pre+1,in,k);
	b->right=CreatTree(pre+k+1,p+1,n-k-1);//左右子树遍历
	return b;
}
int BTHigh(BTNode *BT)
{
	int m,n;
	if(BT==NULL) return 0;
	m=BTHigh(BT->left);
	n=BTHigh(BT->right);
	if(m>n) return m+1;
	else return n+1;
}end for

2.3.2

编译错误：函数{} 漏掉了
遇到的问题：开始对于整个的思路不是很清晰，不知道如何让树结构还原，最后明白要重新建树把树的各分支重新定义

3、阅读代码
https://blog.csdn.net/weixin_39148042/article/details/80960356#
3.1 题目
介绍代码解决问题
用C语言完成二叉树的建立，先序遍历二叉树结构
3.2 解题思路
定于左右孩子树分支--> 建树 -->对树中结构进行遍历-->先序输出 ///代码比较长和复杂，大体用了很多队列 栈和树结构的知识
3.3 代码截图

3.4 学习体会
启发:在解决特定问题的时候，栈队列树结构综合运用非常重要，程序的可读性和可玩性更高