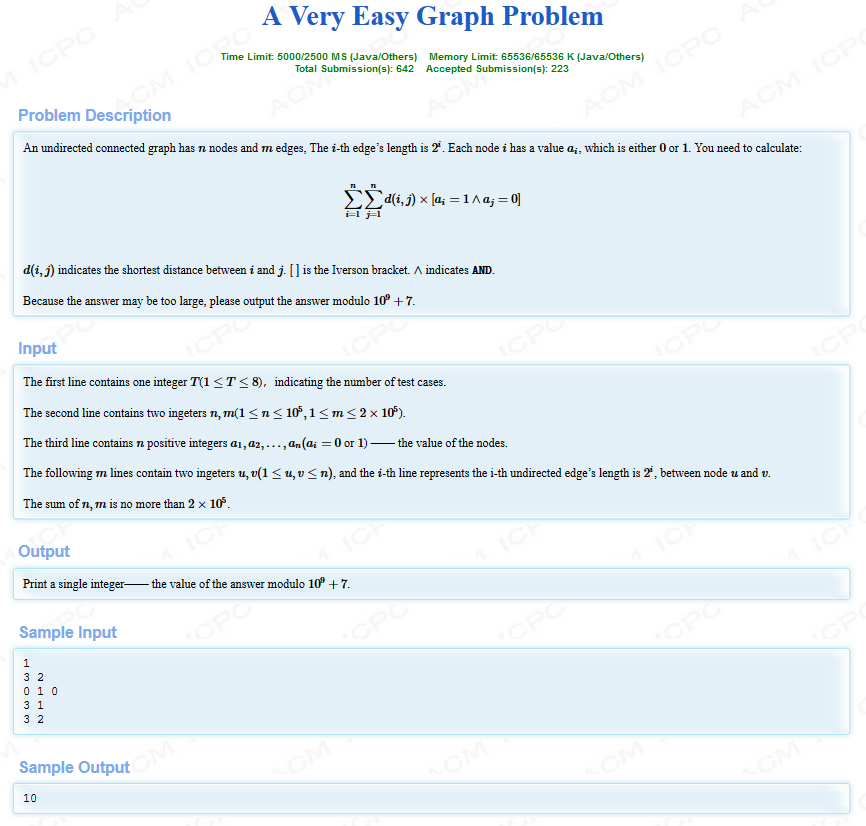
题解:
当时最初我想的是俩个for循环,每个点都跑一次dijstra,答案当然超时
看了题解后发现忽略了第 i 条边的长度是 2^i 这个重要信息提示, 这个的意思是u -> v 只要能通过前 i-1 条边到达,就绝对不会走第 i 条边,因为(2^1 + 2^2 + ... + 2^(i-1) < 2^i,所以俩个点的最短距离,就是最小生成树中俩个点的距离
所以这个题变成了一个最小生成树的题,并且使用Kruskal算法建立,利用并查集维护一下.(对于Kruskal算法,在本文的最后会附上简介和代码)
然后本题给的 n 个顶点都有对应的值,(0,1),把点分为0点,或者1点,题目中的那个式子就是计算所有1点到0点的距离
现在有了最小生成树,如何来计算这个式子呢?
首先,我们把目光聚集到边上来,式子求的是距离,也就是很多个边的和,当然有些边肯定会重复加很多次,所以我们得计算出经过最短生成树中每条边的次数
我们随便找一个边,它的俩端顶点一个是u, 一个是v,什么时候会经过这条边呢,就是 u 及 u的子树的1点去 v 及v 的子树的0点时会经过v,同理v的也一样
所以我们可以用一个dp[N][2]数组来记录每个顶点及其子树的0点和1点的个数。 (OK,到这里,我们就可以看代码了, 代码的注释很详细哦,当然,不知道Kruskal算法的可以再往底部拉一下,先了解Kruskal算法)
/* 重点:求1所有点到0点的个数 */ #include<iostream> #include<algorithm> #include<vector> #include<cstring> using namespace std; typedef long long ll; typedef pair<ll, ll> P; //first是最短距离,second是顶点的编号 const ll N = 1e5 + 5; const ll mod = 1e9+7; ll s[N], f[N], n, m; //s存该点的val f并查集数组 vector<P> G[N]; //存边i->first, 距离second ll dp[N][2]; //存i点子树0,1的个数 ll one, zero; //存总生成树的0,1个数 inline ll read() { ll x = 0, f = 1; char ch = getchar(); while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); } while(ch>='0'&&ch<='9'){ x = x * 10 + ch - '0'; ch = getchar(); } return x * f; } ll find(ll x) { return f[x] == x ? x : f[x] = find(f[x]); } void init() { one = zero = 0; for (int i = 0; i <= n; i++) { G[i].clear(); //清理边 f[i] = i; dp[i][0] = dp[i][1] = 0; } } void dfs(ll u, ll father, ll &res) { dp[u][s[u]]++; //自身结点的val++统计进去 for (ll i = 0; i < (ll)G[u].size(); i++) { ll v = G[u][i].first; if (v == father) continue; //不遍历父节点 dfs(v, u, res); //遍历结束后从底层向上更新信息 dp[u][1] += dp[v][1]; dp[u][0] += dp[v][0]; } for (int i = 0; i < (ll)G[u].size(); i++) { ll v = G[u][i].first; if (v == father) continue; /* 计算经过u-v这条边的贡献值 这条边的子树就是以v为根的树 所以该点的贡献值就是 res += (v点及其子树内0点的个数*(总1点个数 - v点及其子树1点的个数))*cost(u-v) res += (v点及其子树内1点的个数*(总0点个数 - v点及其子树0点的个数))*cost(u-v) */ res = (res+dp[v][0]*(one-dp[v][1])%mod*G[u][i].second)%mod; res = (res+dp[v][1]*(zero-dp[v][0])%mod*G[u][i].second)%mod; } } int main() { ll t = read(); while (t--) { n = read(), m = read(); init(); for (ll i = 1; i <= n; i++) { cin >> s[i]; if (s[i]) one++; else zero++; } ll cost = 1; for (ll i = 1; i <= m; i++) { ll u = read(), v = read(); cost = 2 * cost % mod; if (find(u) == find(v)) continue; //建边 G[u].push_back({v, cost}); G[v].push_back({u, cost}); f[find(u)] = find(v); } //从1开始dfs ll res = 0; dfs(1, -1, res); cout << res << " "; } }
Kruskal算法
Kruskal算法总是维护无向图的最小生成森林。最初,你可以认为该森林没有边,每个节点各自构成一颗仅包含一个节点的树,然后从已知的边(假设m条)中寻找权值最小的边加入其中,并且这条边的俩个端点属于生成森林中俩颗不同的树(不连通)。连通情况使用并查集维护。
具体过程
- 最小生成树(Kruskal算法)
- 1.建立并查集,每个点各自构成一个集合
- 2.把所有边按照权值大小从小到大排列,依次扫描每条边
- 3.若x,y属于同一集合(连通),则忽略这条边,继续扫描下一条边
- 4.否则,合并x,y所在的集合,并把z累加到答案中
- 5.所有便扫描完成后,第4步中处理过的边就构成了最小生成树
1 //最小生成树(Kruskal算法) 2 /* 3 1.建立并查集,每个点各自构成一个集合 4 2.把所有边按照权值大小从小到大排列,依次扫描每条边 5 3.若x,y属于同一集合(连通),则忽略这条边,继续扫描下一条边 6 4.否则,合并x,y所在的集合,并把z累加到答案中 7 5.所有便扫描完成后,第4步中处理过的边就构成了最小生成树 8 */ 9 #include<iostream> 10 #include<algorithm> 11 using namespace std; 12 13 struct rec{int x, y, z;}edge[500010]; 14 int fa[100010], n, m, ans; //fa并查集数组 15 bool operator < (rec a, rec b) { 16 return a.z < b.z; 17 } 18 19 int find(int x) { 20 return fa[x] == x ? x : fa[x] = find(fa[x]); 21 } 22 23 int main() { 24 cin >> n >> m; 25 for (int i = 1; i <= m; i++) { 26 cin >> edge[i].x >> edge[i].y >> edge[i].z; 27 } 28 sort(edge+1, edge+m+1); //按照边权排序 29 for (int i = 1; i <= n; i++) fa[i] = i; //并查集初始化 30 31 for (int i = 1; i <= m; i++) { 32 int x = find(edge[i].x); 33 int y = find(edge[i].y); 34 if (x == y) continue; 35 else { 36 fa[x] = y; 37 ans += edge[i].z; 38 } 39 } 40 cout << ans << " "; 41 }