本文整理来源 《轻松学算法——互联网算法面试宝典》/赵烨 编著
栈
什么是栈
栈是有着特殊规则的数据结构,栈有着重要的一个特点——后进先出(LIFO, Last In First Out),也可以叫做先进后出(FILO, First In Last Out),我们无论如何只能够从一端去操作元素。
栈又叫做堆栈(Stack), 这里说明一下不要将它和堆混淆。实际上堆和栈是两种不同的概念,栈是一种只能在一段进行插入和删除的线性数据结构。
一般来说,栈主要有两个操作:一个是进栈(PUSH),又叫作入栈、压栈;另一个是出栈(POP),或者叫作退栈。
栈是一种比较简单的数据结构。
栈的存储结构
栈一般使用一段连续的空间进行存储,通常预先分配一个长度,可以简单地使用数组去实现。
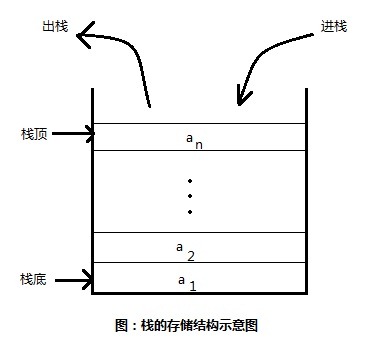
栈只有一个方向可以对栈内的元素进行操作,而从栈中最下面的一个元素称为栈底,一般是数组的第0个元素,而栈顶是栈内最后放入的元素。
一般而言,定义一个栈需要初始的大小,这就是栈的初始容量。当需要放入的元素大于这个容量,就需要扩容。
栈出入元素的操作如下。例如我们初始化一个长度为10的数组,并想其中放入元素,根据栈的定义,只能从数组的一端放入元素,我们设定这一段为数组中较大下标方向。我们放入第一个元素,由于栈内没有元素,我们第一个元素落到数组的第0个下标的位置上;接着放入第二个元素,第二个元素该放入到下标为1的位置上;以此类推,之后我们放入第五个元素时,放入栈中的下标第4个位置上。现在进行出栈操作,出栈智能从一端操作,我们之前设定只能从下标较大的方向操作,因此需要确定数组中下标最大的方向中存在栈元素的位置下标是多少。我们一般会在栈中做个计数器来记录这个值。现在栈中有5个元素,所以讲数组中的第五个位置也就是下标为4的元素出栈。此时数组中只剩下4个元素了。
public class Stack<T> {
private int size = 0;
private static final int DEF_INITIAL = 10;
private Object[] array;
public Stack() {
this(DEF_INITIAL);
}
public Stack(int init) {
if (init <= 0) {
init = DEF_INITIAL;
}
array = new Object[init];
}
/**
* 入栈
*
* @param item 入栈元素
*/
public void push(T item) {
if (size == array.length) {
array = Arrays.copyOf(array, size * 2);
}
array[size++] = item;
}
/**
* 获取栈顶元素,但是没有出栈
* @return 栈顶元素
*/
@SuppressWarnings("unchecked")
public T peek(){
if (size == 0){
throw new IndexOutOfBoundsException("栈顶已经空");
}
return (T) array[size - 1];
}
/**
* 出栈,同时获取栈顶元素
* @return 栈顶元素
*/
public T pop(){
T item = peek();
//直接使元素个数减1,不需要真的清除,下次入栈会覆盖旧元素的值
size--;
return item;
}
/**
* 栈是否满了
* @return 栈是否满了
*/
public boolean isFull(){
return size == array.length;
}
/**
* 栈是否为空栈
* @return 是否为空栈
*/
public boolean isEmpty(){
return size == 0;
}
public int size(){
return size;
}
}
在实现思考当中,第一步是写出来,第二步是扩容,第三步是考虑到异常情况。一个数据结构的实现或多或少总会有些东西可以扩展的,想到多少写多少,在面试或笔试一定会有所加分的。
测试代码:
public class StackTest {
@Test
public void main(){
//为了查看效果,初始数组长度设置为1
Stack<Integer> stack = new Stack<>(1);
stack.push(1);
stack.push(2);
//栈内的元素为2,数组长度也为2
Assert.assertEquals(2,stack.size());
stack.push(3);
//栈内元素个数为3,当前数组长度为4
Assert.assertEquals(3,stack.size());
Assert.assertEquals(4,stack.getLength());
//获取栈顶元素,为3,但是没有出栈
Assert.assertEquals(3,(int)stack.peek());
Assert.assertEquals(3,stack.size());
//栈顶元素出栈,返回3
Assert.assertEquals(3,(int)stack.pop());
//栈顶元素出栈,返回2
Assert.assertEquals(2,(int)stack.pop());
//出栈2次,栈内元素为1
Assert.assertEquals(1,stack.size());
}
}
栈的特点
栈的特点显而易见,只能在一段操作,遵循先进后出或者后者先出的原则。
栈的使用场景
逆序输出
由于栈具备先进后出的特点,所以逆序输出是其中一个非常简单的应用。首先把所有的元素按照元素入栈,然后把所有的元素出栈并输出,轻松实现逆序输出。
语法检查,符号成对出现
在编程语言中,一般括号都是成对出现的,比如“[”和“]”“{”和“}”“(”和“)”“<”和“>”(这里排除大于小于号的作用).
凡是遇到括号的前半部分,即为入栈符号(push);凡是遇到括号的后半部分,就比对是否与栈顶元素相匹配(peek),如果相匹配则出栈(pop),否则就是匹配出错。
数制转换(将十进制的数转换为2-9的任意进制数)
通过求余法,可以将十进制数转换为其他进制,比如转为8进制,则将原十进制数除以8,记录余数,然后继续将商除以8,一直到商等于0为止,最后将余数倒着写出来就行了。
常听说到编程语言调用中的“函数栈”,就是在我们调用方法时计算机会执行PUSH方法,记录调用,在return时也就是方法结束之后,执行POP方法,完成前后对应