树、二叉树基础

版权声明：本文为博主原创文章，转载，请注明出处。若是商业用途，请事先联系作者。 https://blog.csdn.net/zhangxiangDavaid/article/details/36189717

前言

前面介绍的栈、队列都是线性结构(linear structure)。

而树是非线性结构(non-linear structure)。因此，树中的元素之间一般不存在相似于线性结构的一对一的关系。很多其它地表现为多对多的关系。

直观地看，它是数据元素(在树中称为节点)按分支关系组织起来的结构。显然，树形结构是比线性结构更复杂的一种数据结构类型。

一、树

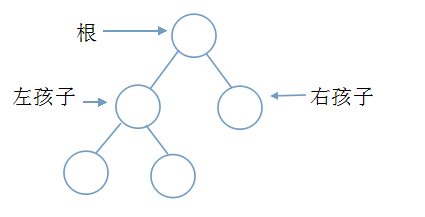
树的定义：树是含有n个节点的有穷集合。当中有一个节点比較特殊称为根节点。

在图示树时，用一条边连接两个有逻辑关系的节点。这个关系被称为父子关系。

二、二叉树

二叉树(Binary Tree)由节点的有限集合构成。这个集合或者为空集，或者为由一个根节点(root)和两棵互不相交，分别称为这个根的左子树(left subtree)和右子树(right subtree)的二叉树组成的集合。

一棵二叉树的示意图：

三、树和二叉树的主要差别

1. 树中节点的最大度数没有限制，而二叉树节点的度不超过2。

2. 树中节点的孩子节点。无左右之分，而二叉树中是有区分的，即孩子是有差别的：左孩子、右孩子，且次序不可颠倒。
3. 树的结点个数至少为1，而二叉树的结点个数能够为0。

四、常见概念

1. 节点的度：某节点的度定义为该节点孩子节点的个数。
2. 叶子节点：度为0的节点。
3. 树的度：一棵树中。最大的节点的度称为树的度。

   
   

4. 节点的高度：从该节点起到叶子节点的最长简单路径的边数。

   (简单路径：无反复边的路径)

5. 树的高度：根节点的高度。

6. 节点的层数：从根開始定义起。根为第1层，根的子节点为第2层，以此类推。

7. 数的层数：根节点的层数。

8. 节点的深度：即该节点的层数。
9. 树的深度：根节点的深度。
10. 外节点：叶子节点。
11. 内节点：除叶子节点之外的节点。
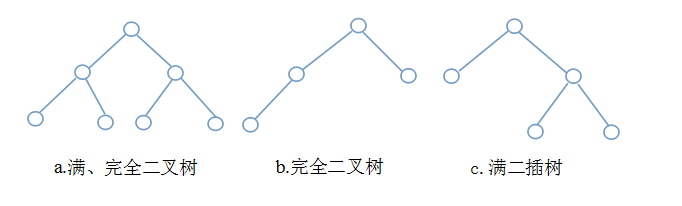
12. 满二叉树：二叉树中节点的度仅仅能是0或2。

13. 全然二叉树：除最后一层。每一层的节点数都达到最大。最后一层若是没满，则节点集中在左边，空的仅仅能是右边。
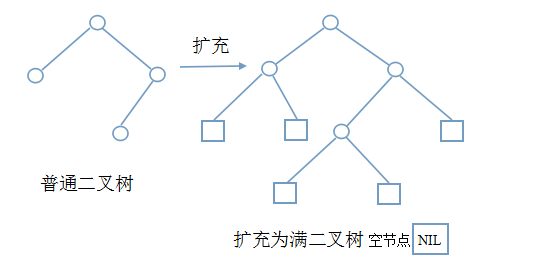
14. 扩充二叉树：对二叉树中度为1的节点和叶子节点加入空节点，使之成为满二叉树。

注：关于树深度、层数、高度的定义会有不同的说法：有从0開始计数的，也有从1開始计数的。从哪儿開始计数不是关键，关键在于一致性，量的写法要一致。

五、几个量的关系

1. 对于二叉树，根节点是第一层，则第i层至多有个结点。若共同拥有k层，则最多有节点个。
2. 按层次顺序对一棵有n个节点的全然二叉树的全部节点从0到n-1编号。

   若父节点的编号是i。则左孩子的编号是2*i+1，右孩子的编号是2*i+2。(当然，这是在存在左右孩子的情况下)。相同的，若孩子(不管左右孩子)节点是i，则父节点是(i-1)/2。

3. 对于一棵满二叉树。外部节点或者说是叶子节点数是n，则内部节点数是n-1。
4. 对于一棵二叉树，用ni表示度为i的节点个数。则n0=n2+1。证明例如以下：总节点数n=n0+n1+n2。

   用e表示边数。则n=e+1，这是由于除根节点外，每个节点都和一条边相应。同一时候，e=2n2+n1。推出n0+n1+n2=2n2+n1+1，化简即得n0=n2+1。

   这个结论用语言表述：二叉树中，叶子节点比度为2的节点多一个。

5. 有n个节点的全然二叉树，树高度，即logn向下取整，高度从0计数。
6. 在二叉树中。第i层的第一个节点(最左边的节点)的编号是，层数从0计数。这个量在选择排序：树形选择中用到了。

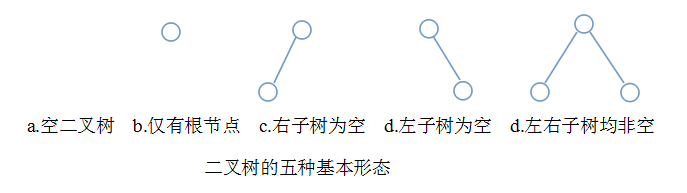
六、示意图

专栏文件夹：

• 数据结构与算法文件夹
• c指针