Codeforces Round #245 (Div. 2)

版权声明：本文为博主原创文章，未经博主同意不得转载。 https://blog.csdn.net/yew1eb/article/details/25609981

A Points and Segments (easy)

 智商题。（智商捉急~）

/***********************************************************
 *分析：仅仅要按Xi从小到大染成1010101010... ，
 *1、0间隔的的序列就能保证对于随意区间[l, r]中1的个数和0的个数之差小于等于1。
 *注意：因为输入的Xi可能是无序的。全部要两次排序处理。
 **********************************************************/
#include <cstdio>
#include <algorithm>
using namespace std;

const int maxn = 200 + 5;

struct node  {
    int id;
    int x;
    int val;
};
node a[maxn];
int n, m;


bool cmp_x(const node &a,const node &b)
{
    return a.x < b.x;
}
bool cmp_id(const node &a,const node &b)
{
    return a.id<b.id;
}
int main()
{
    int i, l, r;
    scanf("%d%d",&n,&m);
    for(i=0; i<n; ++i) 
    {
        scanf("%d",&a[i].x);
        a[i].id = i;
    }
    for(i=0; i<m; ++i)
        scanf("%d%d",&l, &r);
    sort(a, a + n, cmp_x);
    for(i=0; i<n; ++i) 
        a[i].val =  i&1;
    sort(a, a + n, cmp_id);
    for(i=0; i<n; ++i)
        printf("%d ", a[i].val);

    return 0;
}

B Balls Game

枚举

/************************************************
 *分析：枚举插入点，然后用循环模拟消除操作
 ************************************************/
#include <stdio.h>
int n, k, x;
int a[100+5];

int main()
{
    int i, l, r, cnt, ret, ans = 0;
    scanf("%d%d%d",&n, &k, &x);
    for(i=0; i<n; ++i)
        scanf("%d",&a[i]);

    for(i=0; i<n; ++i)
    if(a[i]==x)
    {
        l = r = i;
        cnt = 0;
        while(a[l] == a[r]) 
        {
            ret = 2;
            while(l > 0 && a[l-1] == a[l]) { l--; ret++;}
            while(r < n-1 && a[r+1] == a[r]) {r++; ret++;}
            --l; ++r;
            if(ret<3) break;
            cnt += ret;
            if(l < 0 || r >= n) break;
        }
        if(cnt-1 > ans) ans = cnt-1;
    }
    printf("%d
", ans);
    return 0;
}

C Xor-tree

建树后DFS

/******************************
 * 分析：题意简单
 * 在树上进行简单的操作
 ******************************/
#include <cstdio>
#include <vector>
using namespace std;

const int maxn = 100000 + 10;
vector<int> Edge[maxn];
int cnt = 0, ans[maxn];
int n, a[maxn], b[maxn];

void dfs(int rt, int pre, int p1, int p2)
{
    if( a[rt]^ p1 != b[rt])
    {
        ans[cnt++] = rt;
        p1 = 1- p1;
    }

    for(int i=0; i<Edge[rt].size(); ++i)
    {
        int &e = Edge[rt][i];
        if(e == pre) continue;
        dfs(e, rt, p2, p1);
    }
}

int main()
{
    int i, x, y;
    scanf("%d",&n);
    for(i=1; i<n; ++i)
    {
        scanf("%d%d",&x,&y);
        Edge[x].push_back(y);
        Edge[y].push_back(x);
    }
    for(i=1; i<=n; ++ i) scanf("%d",&a[i]); for(i=1; i<=n; ++i) scanf("%d",&b[i]);
    dfs(1, -1, 0, 0);
    printf("%d
", cnt);
    for(i=0; i<cnt; ++i)
        printf("%d
", ans[i]);
    return 0;
}

D Working out

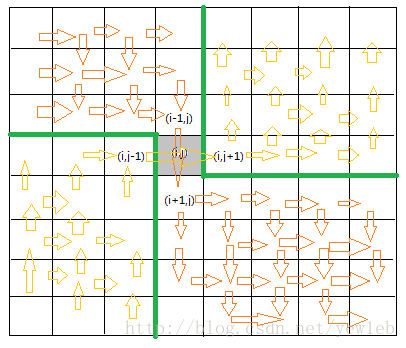
先递推出每个点(i,j)到四个顶点{(n,m), (n,1), (1,m), (1,1) }的最大权值和。 然后枚举交点。 对于每个交点仅仅有例如以下图两种情况满足题意仅仅有一个交点。

#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 1000  + 100;
int n, m, a[maxn][maxn], f1[maxn][maxn], f2[maxn][maxn], f3[maxn][maxn], f4[maxn][maxn], ans;

int main()
{
    int i, j;
    scanf("%d%d",&n, &m);
    for(i=1; i<=n; ++i)
        for(j=1; j<=m; ++j)
            scanf("%d",&a[i][j]);

    for(i=1; i<=n; ++i)
        for(j=1; j<=m; ++j)
            f1[i][j] = max(f1[i-1][j], f1[i][j-1]) + a[i][j];

    for(i=1; i<=n; ++i)
        for(j=m; j>=1; --j)
            f2[i][j] = max(f2[i][j+1], f2[i-1][j]) + a[i][j];

    for(i=n; i>=1; --i)
        for(j=1; j<=m; ++j)
            f3[i][j] = max(f3[i][j-1], f3[i+1][j]) + a[i][j];

    for(i=n; i>=1; --i)
        for(j=m; j>=1; --j)
            f4[i][j] = max(f4[i][j+1], f4[i+1][j]) + a[i][j];

    ans = 0;
    for(i=2; i<n; ++i)
        for(j=2; j<m; ++j)
            ans = max(ans, max(f1[i-1][j] + f2[i][j+1] + f3[i][j-1] + f4[i+1][j], 
			f1[i][j-1] + f2[i-1][j] + f3[i+1][j] + f4[i][j+1]) );
    printf("%d
", ans);
    return 0;
}

E Guess the Tree

load....