更好的阅读体验
更好的阅读体验
更好的阅读体验
这篇题解主要讲代码实现,思路可能需要照着代码理解,请慎重阅读
两张图片挂了,重新传了一遍。
最后代码写出来3.5Kb,不到150行,相对来说还是挺短的...
给定一棵 (n) 个节点的树,边带权,编号 (0 sim n-1),需要支持五种操作:
C i w将输入的第 (i) 条边权值改为 (w)N u v将 (u,v) 节点之间的边权都变为相反数SUM u v询问 (u,v) 节点之间边权和MAX u v询问 (u,v) 节点之间边权最大值MIN u v询问 (u,v) 节点之间边权最小值
保证任意时刻所有边的权值都在 ([-1000,1000]) 内。
前置知识:树链剖分。
主要讲代码实现。
首先因为树的编号不好看,所以都加一。
然后分操作考虑。
数组定义写在前面:
dep:深度
fa:父亲结点
sz:子树大小
son:重儿子
id:结点对应的dfs序
rk:dfs序对应的结点
ID[i]:用来承接 [数组中存储的编号为id 的边] 的信息的点编号
a[u]:点u承接下来的信息
top:重链顶端
线段树结点(动态开点):{lc,rc(左右儿子),w(区间和),mx,mn(极值),f(=±1,表示未下传的取相反数标记)}
Part 0 整体思路
因为传统的重链剖分是把信息对于点来储存,对于边考虑怎么算。
于是就有一个很朴素的想法,把每条边的边权下沉到对应的点。
也就是像下面这样,用u号点来承接边(f→u)的权值。

因为输入的边不一定是从父亲到儿子,所以我们考虑把输入的第 (i) 条边记录到数组里第 (2i,2i+1) 的位置。
这样我们在重链剖分dfs的时候,假设通过点 (u) 走到了 (v=to[i]) ,那么我们就承接边权到 (v) ,即 a[v]=val[i],同时为了方便修改边权落实到修改点权,记录 ID[i/2]=v。
然后考虑这样会对查询操作有什么影响,显然如下图:
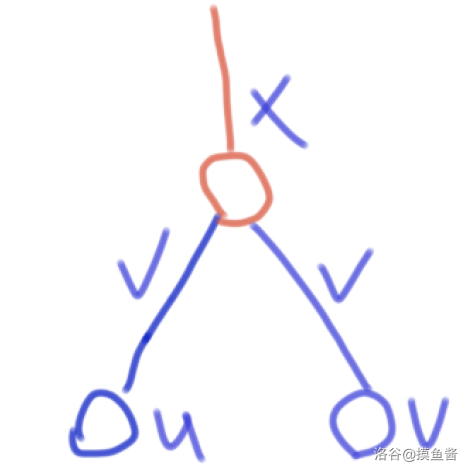
我们要求 (u,v) 之间的边权信息,但是常规的重链剖分会把上面打×的边也统计。
这个解决就考虑树链剖分查询操作的时候,最终会有一段对于 id[x],id[y] 的查询 (id[x]<id[y]) ,是在同一条重链上的,那么对应的 id[x]+1,id[y] 就不包括它们的LCA x。
于是这个问题也解决了。就可以开始干代码了。
先有三个基础的函数放在这里。
void up(int k){
t[k].w=t[ls].w+t[rs].w,t[k].mx=max(t[ls].mx,t[rs].mx),t[k].mn=min(t[ls].mn,t[rs].mn);
}
void down(int k){
if(t[k].f==1)return;
opp(ls),opp(rs),t[k].f=1;
}
void opp(int k){
swap(t[k].mn,t[k].mx),t[k].mn*=-1,t[k].mx*=-1,t[k].w*=-1,t[k].f*=-1;
}
分别是线段树的 push_up,push_down和把结点 (k) 整体取反。
这里说下整体取反。显然就是新的最小值等于原来最大值的相反数,最大值同理。权值和就等于之前的相反数。
注意:这里的 (f) 是还没有传下去的标记,不能抵消将要打在自己身上的取反操作。
Part 1 单点赋值
这个是基础线段树操作,输入把边 (u) 赋值为 (w) ,那就把线段树上的 id[ID[u]] 赋值成 (w) 。
void modify(int k,int l,int r,int pos,int x){//单点pos赋值x
if(l==r)return t[k].w=t[k].mx=t[k].mn=x,void();
down(k);
int m=l+r>>1;
if(pos<=m)modify(ls,l,m,pos,x);
else modify(rs,m+1,r,pos,x);
up(k);
}
Part 2 两点路径取相反数
先是常规套路,把线段树上的一段给取相反数。
这个显然也是基础的线段树的操作。
void md(int k,int l,int r,int x,int y){//一段取反
if(x<=l&&r<=y)return opp(k);
down(k);
int m=l+r>>1;
if(x<=m)md(ls,l,m,x,y);
if(y>m)md(rs,m+1,r,x,y);
up(k);
}
然后也是重链剖分的板子。
注意这里的 if(x==y)return; ,因为如果最后x,y重合,表示它们都是输入的x,y的LCA,那么贡献就不能记录到答案里。
void modi(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
md(1,1,n,id[top[x]],id[x]);
x=fa[top[x]];
}
if(x==y)return;
if(id[x]>id[y])swap(x,y);
md(1,1,n,id[x]+1,id[y]);
}
Part 3 三种查询
发现这三种查询本质相同。
于是代码基本就和树链剖分板子一样了。
void ask_xds(int k,int l,int r,int x,int y,int op){//1:sum 2:max 3:min
if(x<=l&&r<=y){
if(op==1)res+=t[k].w;
if(op==2)res=max(res,t[k].mx);
if(op==3)res=min(res,t[k].mn);
return;
}
down(k);
int m=l+r>>1;
if(x<=m)ask_xds(ls,l,m,x,y,op);
if(y>m)ask_xds(rs,m+1,r,x,y,op);
up(k);
}
int ask(int x,int y,int op){//1:sum 2:max 3:min
int ans=op==1?0:(op==2?-1e9:1e9);
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
res=op==1?0:(op==2?-1e9:1e9);
ask_xds(1,1,n,id[top[x]],id[x],op);
if(op==1)ans+=res;
if(op==2)ans=max(ans,res);
if(op==3)ans=min(ans,res);
x=fa[top[x]];
}
if(id[x]>id[y])swap(x,y);
if(x==y)return ans;
res=op==1?0:(op==2?-1e9:1e9);
ask_xds(1,1,n,id[x]+1,id[y],op);
if(op==1)ans+=res;
if(op==2)ans=max(ans,res);
if(op==3)ans=min(ans,res);
return ans;
}