练了几天数学期望的基础题,记录一下学习心得。
前置知识:
我们一般用E(X)表示事件X的数学期望。那么我们有(E(x)=sum(a_i*p_i)),其中(p_i)是i事件发生的概率,(a_i)是事件i对应的权值。
举个例子,扔一次骰子得到的点数(E(x)=frac{1}{6}*1+frac{1}{6}*2+frac{1}{6}*3+frac{1}{6}*4+frac{1}{6}*5+frac{1}{6}*6=3.5)。
但是在很多情况下,我们并不能直接枚举所有这样的i事件来求得期望,具体可以看接下来前言中的例题。
前言
首先要从对极限情况的死磕里跳出来,比如NOIP2013的这道初赛题:

如果死磕某种一直在某个荷叶上不往回跳的情况,那可能难以想到正确的解法,虽然这种情况确实有可能发生。
先设(f_i)为(i)号荷叶跳到1号荷叶的期望步数,那我们就有(f_k=(sum^k_{i=1}frac{f_i}{k})+1),从题目意义上来说,就是 (k) 号节点会等概率跳到前面的荷叶上,并且会花费一步的代价,这样就可以算出答案是(frac{37}{12})。
最重要的是设计期望的状态。很多较简单的转移就自然出来了。
比如这样一个简单的例题:假设硬币扔出两面的概率相同,连续扔出n个正面期望需要扔多少次硬币?
这道题目显然也不能够直接枚举出现某种情况的概率,所以我们考虑设计状态,用递推来解决这个问题。
我们设(E_n)为扔出连续n个正面硬币的期望次数,那么就有(E_n=frac{1}{2}(E_{n-1}+1)+frac{1}{2}(E_{n-1}+1+E_{n})),从实际意义来说,就是有一半的几率可以由[连续n-1枚正面再扔一次正面]转移,一半的几率由[连续n-1枚正面再扔一次反面,再连续扔n枚正面]转移,化一下式子就可以得到(E_n=2E_{n-1}+2)。
相信你已经学会了期望的基本状态设计和转移,接下来就是例题了。
在前置知识中我们接触了扔一枚6面的骰子的期望点数,那么就来看看扔n枚m面骰子的期望最大点数吧(Little Pony and Expected Maximum)。n,m≤1e5。
假设扔到m面的概率均为(frac{1}{m}),扔n次就会有(m^n)种情况,每种情况出现概率均等,需要求每一轮扔到的最大值乘上(frac{1}{m^n}),但显然是不能枚举所有情况的。
正难则反,那么我们考虑每轮最大值的情况。
先假设每轮的最大值都是(m),然后减去实际最大值小于(m)的情况。举个例子,考虑(n)次都只扔出([1,m-1])的概率,显然是((frac{m-1}{m})^n),对应需要减去的权值是1。同理,(n)次都只扔出([1,m-i],ile m-1)对答案的贡献就是(-(frac{m-i}{m})^n),i从1到m-1枚举,但是要考虑i时的情况都被i-1时的包括,所以权值省去即可,原因可以自行举例理解。
[collapse status="false" title="code"]
#include<bits/stdc++.h>
using namespace std;
int main(){
int m,n;
scanf("%d%d",&m,&n);
double res=m;
for(int i=1;i<m;i++){
res-=pow((m-i*1.0)/m,n);
}
printf("%.8lf",res);
return 0;
}
[/collapse]
Archer,一道不错的练手题。
有两个人比赛射箭,A有(frac{a}{b})的概率射中,B有(frac{c}{d})的概率射中,第一个射中的人获胜,从A开始轮流射箭,问A获胜的概率。
我们设(A=frac{a}{b},B=frac{c}{d},A'=1-A,B'=1-B)。
那么A获胜的情况无非就是"A,A'B'A,A'B'A'B'A...",设(K=A'·B'),那就是"A,KA,K^2A...",显然就是求(sum_{i≥0}K^iA=A*sum_{i≥0}K^i),后面那个显然就是一个无穷等比数列求和。
于是输出的就是(frac{A}{1-K})。
一道有趣的题:Falling Anvils,
给定(a,b),(p∈[0,a],q∈[-b,b]),在(p,q)随机取值的情况下,求方程(x^2+sqrt p·x+q=0)有实数根的概率。
显然就是要求(pge4q)的概率,我们让(q∈[-4b,4b]),让(pge q)即可。
让((p,q))放到平面直角坐标系中,显然满足要求的点的坐标在直线(y=x)下方,于是分下图两种情况考虑答案。
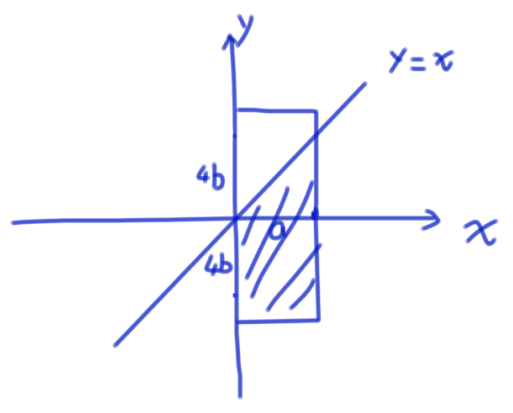
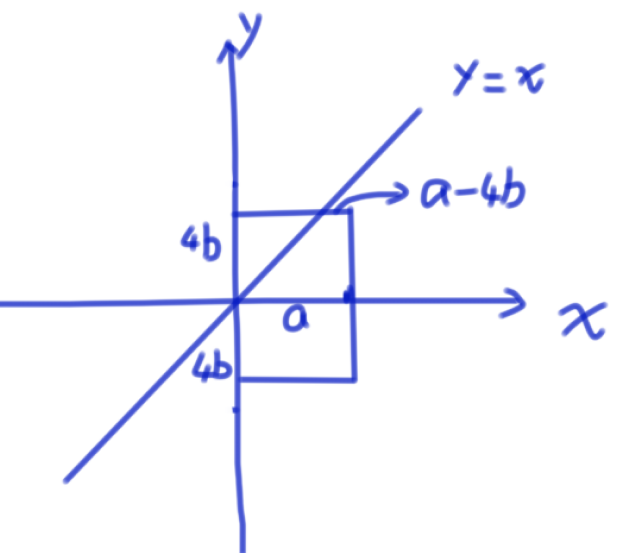
显然,答案就分(a<4b)时的(frac{(8b+a)a}{2*8ab})和(a>4b)时的(frac{4ab+frac{(2a-4b)b}{2}}{8ab}),相等时随便归到一类即可。