【题解】在你窗外闪耀的星星-C++

题目
题目描述
飞逝的的时光不会模糊我对你的记忆。难以相信从我第一次见到你以来已经过去了3年。我仍然还生动地记得，3年前，在美丽的集美中学，从我看到你微笑着走出教室，你将头向后仰，柔和的晚霞照耀着你玫瑰色的脸颊。我明白，我已经沉醉于你了。之后，经过几个月的观察和窥探，你的优雅与智慧，你对待生活的态度和你对未来的愿望深切地在我心中留下了印象。你是迷人的阳光女孩，我总是梦想着与你分享余生。唉，实际上你远远超过了我最疯狂的梦想。我不知道如何桥起我与你之间的鸿沟。所以我没有任何计划，仅仅只是等待，等待一个适当的机会到来。直到现在，毕业的到来，我意识到我是个傻瓜，我应该创造机会并且抓住它而不只是等待。

这些日子里，我和我的朋友、室友、同学一个接一个地分开。我仍无法相信，在挥手之后，这些熟悉的面孔很快就会从我们的生活中消失，仅仅留下回忆。我明天就将离开学校。你已经计划远走高飞，追求你的未来，实现你的梦想。如果没有命运，也许我们不会再次相遇。所以今晚，我正在你的宿舍楼下徘徊，希望能偶然遇见你。但矛盾的是，你的美貌一定会使我心跳加速，我笨拙的舌头也许无法吐出一个字。我不记得我曾多少次经过你的宿舍楼，每次都希望看到你出现在阳台上或是窗台上。我不记得这个想法曾多少次在我的脑海中涌出：打电话叫她一起吃晚饭或是聊聊天。但每次，考虑到你的优秀和我的平凡，胆怯的优势超越勇气驱使我静静地离开。

毕业，意味着中学生活的终结。这些光荣与浪漫的时代结束。你可爱的微笑是我原来努力学习的动力，这单相思的爱情会被密封，作为一个我心灵深处的记忆。毕业，也意味着新生活的开始，一个到达光明未来的足迹。我真希望你在国外天天开心，一切顺利。同时，我将努力从幼稚中走出来，变得更加成熟。我的理想将是在现实中追求我的爱与幸福，我永远不会放弃。

再见了，我的公主！

如果有一天，在某个天涯海角，我们有机会相聚，即使是白发苍苍的男人和女人，在那个时候，我希望我们可以成为好朋友来自豪地分享这个记忆，重温年轻快乐的激情。如果这个机会永远没有到来，我希望我是天空中的星星，在你的窗外闪烁。远远地保佑着你，就像一个朋友，每天晚上陪伴在你左右，一同分享甜美的梦亦或是一同经历可怕的梦。

现在问题来了：天空可以理解为一条数轴，在这条数轴上分布着许多颗星星，对于每颗星星都有它的位置Xi和自身的亮度Bi。而窗户所能看到的范围是一个给出的参数W，我们看到的星星也包括窗户边缘的星星。现在，要你求出调整窗户位置后能看到星星的亮度之和最大值。

输入输出格式
输入格式：
一行N,W，分别代表星星的数量和窗户的宽度

余下N行，输入Xi和Bi，代表星星的坐标和亮度

输出格式：
一个数字，代表能看到星星的最大亮度和

输入输出样例
输入样例#1：
6 3
1 2
2 4
3 8
4 4
5 2
1000 1
输出样例#1：
16
说明
样例说明：

 

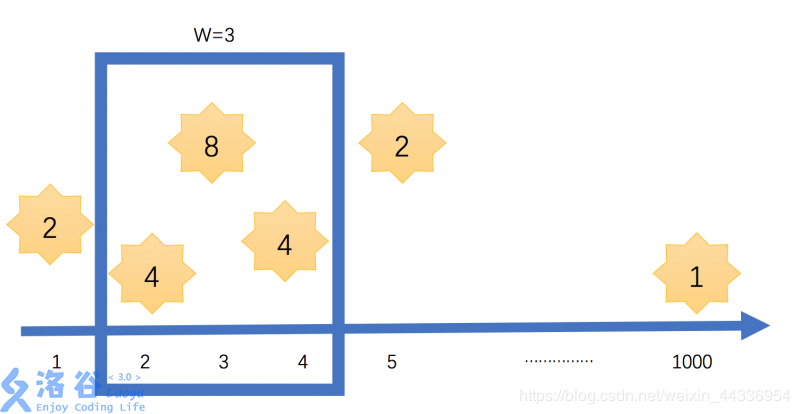
对于10%的数据，W=0（没有边缘）

对于40%的数据，W<=1000

对于100%的数据，N<=100000，W<=100000，Xi<=100000，1<=Bi<=100

除W=0的情况外，W均为>=3的奇数
(题目传送门在这里)

思路
虽然这道题数据很水，用前缀和也可以水过去，但是摸鱼酱还是讲一下正解。
正解树状数组！
这道题目实际就是树状数组模板1的改版
然后主要操作：
添加
区间查询
过程中会用到lowbit操作:
lowbit(x)是x的二进制表达式中最低位的1所对应的值。
比如6的二进制是110,lowbit(6)=2.
其他的就理解下代码了…

代码

#include<bits/stdc++.h>
#define FAST_IN std::ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL)
using namespace std;
int n,w,tree[100010];
int Max=-1; 
int lowbit(int k)
{
    return k&-k;
}
void add(int x,int k)
{
    while(x<=n)
    {
        tree[x]+=k;
        x+=lowbit(x);
    }
}
int sum(int x)
{
    int ans=0;
    while(x>0)
    {
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}
int main()
{
    FAST_IN;
    cin>>n>>w;
    for(int i=1;i<=n;i++)
    {
        int x,y;
        cin>>x>>y;
        add(x,y);
    }
    for(int i=w;i<=100000;i++)
    {
        Max=max(Max,sum(i-1)-sum(i-w-1));
    }
    cout<<Max<<endl;
    return 0;
}