【最小生成树之Kruskal算法】
没有看过的可以先看↑,会更简单。
【模板】最小生成树
这一篇博客主要是介绍另外一种算法:Prim算法。
prim算法就好像是一棵"生成树"在慢慢长大,从开始的一个顶点长到了n个顶点。
总结一下这个算法,将图中所有的顶点分为2类,树顶点(已被选入生成树的顶点)和非树顶点(还未被选入生成树的顶点),接下来要找出一条边添加到生成树,这需要枚举每一个树顶点到每一个非树顶点所有的边,然后最短边加入到生成树,重复操作n-1次,直到所有顶点加入到生成树中。
实现此算法时,比较了dijkstra最短路径算法,在记录的最短距离,不是每个顶点到1号顶点的距离,而是每个顶点到任意一个“树顶点”的最短距离。
时间复杂度:O(n^2)(n为顶点数)
主要思路: 通过依次加入新的最优的店来实现。用dst[i]来表示第i个点加入这棵树所需的代价。
可能有点难理解,那就画图理解:
大概如下一个无向图:
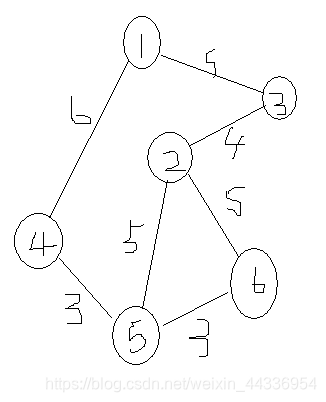
因为从任意一个顶点出发都可以生成这棵最小数,所以我们在代码中都规定从编号为1的定点开始构造。(将1打上标记)同时记录dst[1]=0;(是没有任何代价的,可以自己理解一下)
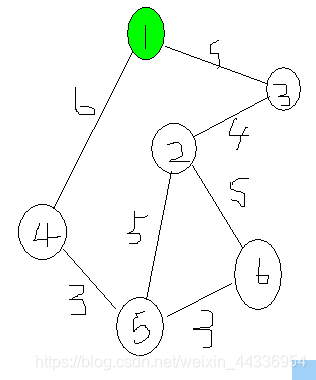
从点1出发,我们可以找到(和点1直接连接的点)有3和4,选择边权值最小的一个(1-3)那么将3也放进已经确定来源的部分(打标记)如下(同时记录dst[3]=5;)
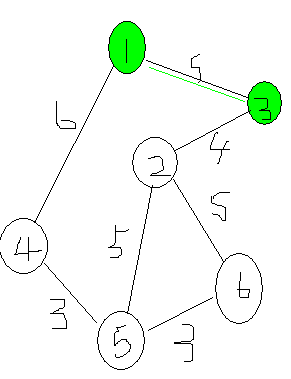
和3有连接的点只有2,那么也打上标记.(记录dst[2]=4)
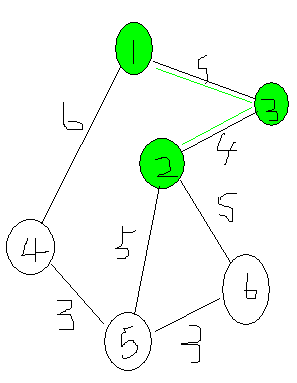
按照循环顺序,应该先找到5(记录dst[5]=5)
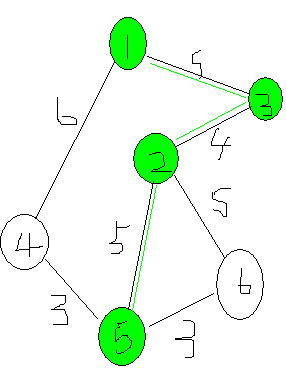
接下来找到4(记录dst[4]=3)
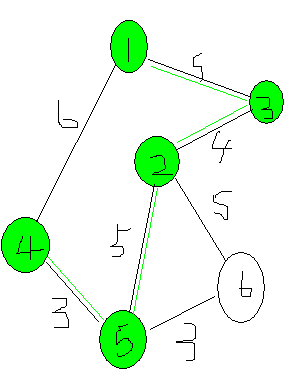
接下来找到点6(记录dst[6]=3(这样最优))
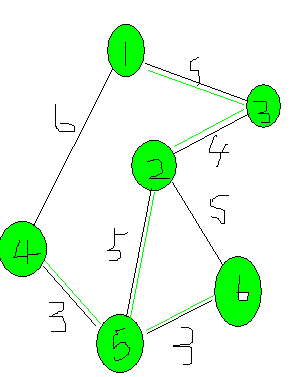
这样,每个点都加入了这棵树,所以任务完成,这棵树的最小生成树形态如下:
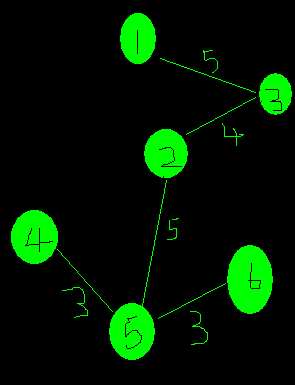
接下来说说代码实现。
根据我们的模拟过程,输入之后先将点1打上标记,然后在和点1有连接的所有点中找到最优点3,然后将点3打上标记,然后在和点3有连接的所有点中找到最优点2.。。。。。
发现过程规律了吗?双重循环即可解决这个问题!
我们用一个结构体+二维vector数组g来记录与点i相连的所有点及其权值。另外为了方便,我还是用pre[i]来表示是点pre[i]连接上点i进入这棵树的。
外层for(i=1->n-1)内层第一个for(j=0->g[lasti].size())确定当前每个点的最优代价(不断更新)内层第二个for(i=1->n)统计最优点即可。
代码如下:
#include<bits/stdc++.h>
using namespace std;
int dst[5010];
int n,m;
bool s[5010];
int pre[5010];
struct node
{
int v,w;
node(){}
node(int vv,int ww)
{
v=vv,w=ww;
}
};
vector<node> g[5010];
void init()
{
for(int i=1;i<=5000;i++)
{
dst[i]=0x7f7f7f7f;
}
}
int main()
{
init();
int a,b,c;
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>a>>b>>c;
g[a].push_back(node(b,c));
g[b].push_back(node(a,c));
}
s[1]=1;
dst[1]=0;
int lasti=1;
for(int k=1;k<n;k++)
{
for(int j=0;j<g[lasti].size();j++)
{
int v=g[lasti][j].v,w=g[lasti][j].w;
if(!s[v]&&w<dst[v])
{
pre[v]=lasti;
dst[v]=w;
//dst[v]+=dst[pre[v]];
}
}
int min_i=0x7f7f7f7f,min_dst=0x7f7f7f7f;
for(int i=1;i<=n;i++)
{
if(!s[i])
{
if(dst[i]<min_dst)
{
min_dst=dst[i];
min_i=i;
}
}
}
lasti=min_i;
s[min_i]=1;
printf("更新点%d加入,父节点%d
",lasti,pre[lasti]);
}
int total=0;
for(int i=1;i<=n;i++)
{
total+=dst[i];
printf("pre[%d]=%d
",i,pre[i]);
}
cout<<total<<endl;
return 0;
}
输入如下数据:
6 7
1 3 5
3 2 4
2 6 5
2 5 5
5 6 3
4 5 3
1 4 6
输出如下:
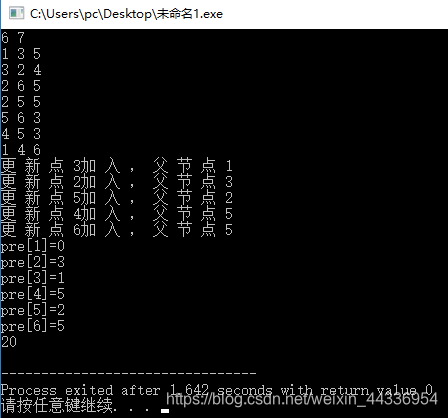
prim算法要嗦的大概就是这些,剩下的需要自己不断理解,希望大家在这条路上越走越远,加油!
ov.