1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
回归算法的含义:

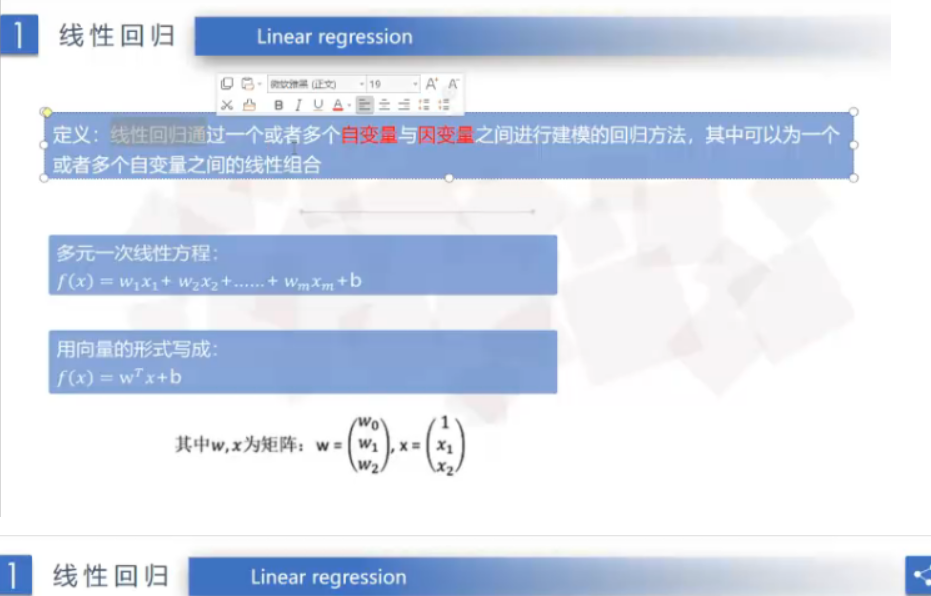
线性回归的含义:
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
答:线性回归的预测模型虽然是一元(线性)方程,但现实中很多应用场景符合这个模型,例如商品的价格与商品的销量之间的关系。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
数据:中财网爬取
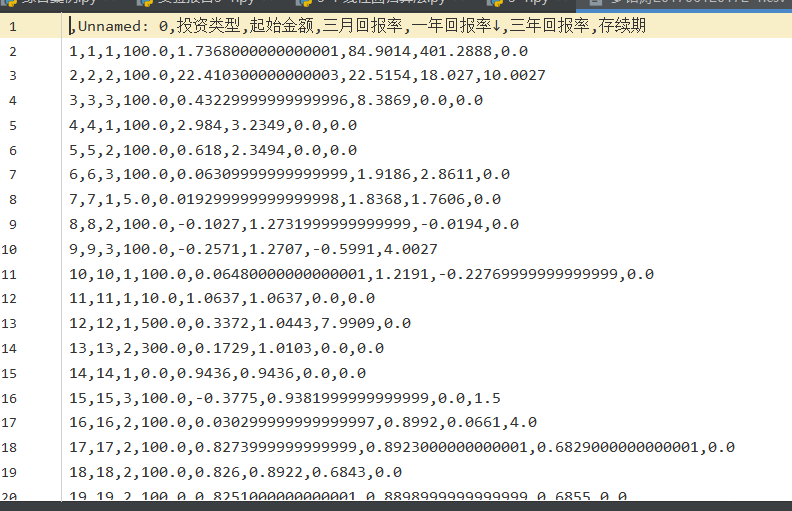
线性回归代码:
print('201706120172,罗镕涛,软件1702') import numpy as np import pandas as pd import matplotlib.pyplot as plt df = pd.read_csv('./data/罗镕涛201706120172-1.csv',encoding='GB2312') df.iloc[:,5] X=df.iloc[:,5]#生成-2*3.14到2*3.14的200个数 Y=df.iloc[:,4]-0.1#将X正弦化,然后加入噪音 np.array(X) np.array(Y) X=X.values.reshape(-1,1)#扁平化,就是features只能为1 Y=Y.values.reshape(-1,1) from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import Pipeline def polynomial_model(degree=1): polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)#生成degree阶多项式 linear_regression=LinearRegression(normalize=True)#线性回归实例化,并且正规化 pipeline=Pipeline([("polynomial_features",polynomial_features),("linear_regression",linear_regression)])#流水线 return pipeline from sklearn.metrics import mean_squared_error degrees=[2,3,5,10]#多项式的阶数 results=[]#结果数组 for d in degrees:#运行四次 model=polynomial_model(degree=d)#生产degree多项式模型 model.fit(X,Y)#将X,Y扔到模型里面去训练 train_score=model.score(X,Y)#得到评分 mse=mean_squared_error(Y,model.predict(X))#计算均方根误差 results.append({"model":model,"degree":d,"score":train_score,"mse":mse})#追加对应数据到results里面 for r in results: print("degree:{};train score:{};mean squared error:{}".format(r["degree"],r["score"],r["mse"])) from matplotlib.figure import SubplotParams plt.figure(figsize=(12,6),dpi=200,subplotpars=SubplotParams(hspace=0.3)) #subplotpars只是控制各下属图形高度上的间距为0.3 for i,r in enumerate(results):#循环四次 fig=plt.subplot(2,2,i+1)#四张图,绘画顺序对应i+1 plt.xlim(-8,8)#每张图的x轴的限制为-8到8,对应上面的-2*3.14到2*3.14 plt.title("LinearRegression degree={}".format(r["degree"]))#标题 plt.scatter(X,Y,s=5,c='b',alpha=0.5)#蓝色的散点 plt.plot(X,r["model"].predict(X),'r-')#预测的曲线
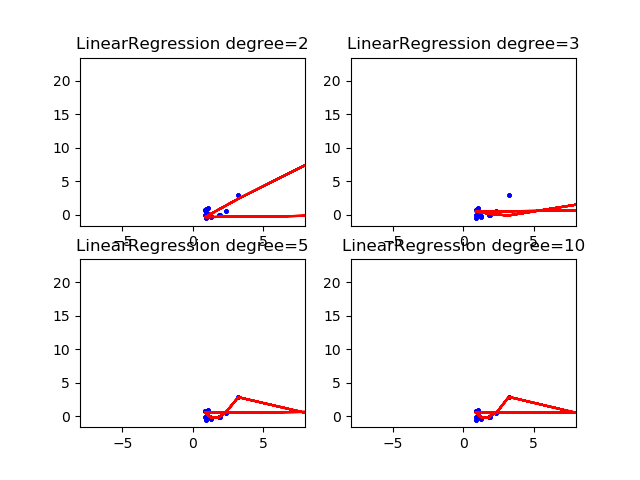
运行结果:
翻译 朗读 复制 正在查询,请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译(国内) 译
翻译 朗读 复制 正在查询,请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译(国内) 译
翻译 朗读 复制 正在查询,请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译(国内) 译