T1:入阵曲

n,m<=400,k<=1e6
分析:
考虑只有一行的情况:
将这一行求前缀和后,一段区间的和x=sum[r]-sum[l-1],如果x%k==0,那么sum[r]%k - sum[l-1]%k == 0
转化一下,也就是说:sum[r]与sum[l-1]在模k的意义下相等。
所以对于一行的来说,O(n)地for一遍,用一个桶记录一下模k意义下的值相同的个数,ans+=cnt[k]*(cnt[k]-1)/2
对于多行的来说,枚举上界和下界,再将这一块子矩阵对列求前缀和压缩成一列,转化成上面的问题。
复杂度:O(n^3)

#include<bits/stdc++.h> using namespace std; #define N 405 #define M 1000005 #define ll long long #define ri register int int n,m,kk,ans=0,t[M],q[M]; ll a[N][N],l[N][N]; int main() { freopen("rally.in","r",stdin); freopen("rally.out","w",stdout); scanf("%d%d%d",&n,&m,&kk); for(ri i=1;i<=n;++i) for(ri j=1;j<=m;++j) scanf("%lld",&a[i][j]); for(ri j=1;j<=m;++j) for(ri i=1;i<=n;++i) l[i][j]=l[i-1][j]+a[i][j];//对列求前缀和 ll ans=0; for(ri i=1;i<=n;++i) for(ri j=i;j<=n;++j){ //memset(t,0,sizeof(t));memset会超时 ll sum=(l[j][1]-l[i-1][1]) %kk,top=0;//将一列压缩成一行,对行求前缀和 for(ri k=1;k<=m;++k){ if(!t[sum]) q[++top]=sum; t[sum] ++;//桶记录 sum=(sum+l[j][k+1]-l[i-1][k+1]) %kk; } ans+=t[0]; for(ri k=1;k<=top;++k) if(t[q[k]]) ans+=(t[q[k]]-1)*t[q[k]]/2,t[q[k]]=0;//清空 } printf("%lld ",ans); return 0; } /* 2 3 2 1 2 1 2 1 2 2 3 2 3 3 3 3 3 3 6 7 5 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 */
T2: 将军令

n<=1e5,k<=20
分析:
从底向上贪心,对于节点最深的点x,选择距离它k的祖先覆盖它一定是最优的。
原因:距离它k的祖先是恰好覆盖x,且覆盖的范围最广的点。
自底向上选点,暴力打标记即可。

#include<bits/stdc++.h> using namespace std; #define N 100005 #define ri register int int tot=0,to[N<<1],nex[N<<1],head[N],fa[N],dep[N],n,kk,vis[N]; struct node{ int dep,u; }; priority_queue<node> q; bool operator < (const node &a,const node &b) { return a.dep<b.dep; } void add(int a,int b) { to[++tot]=b; nex[tot]=head[a]; head[a]=tot; } void dfs1(int u,int ff) { q.push((node){ dep[u],u }); for(ri i=head[u];i;i=nex[i]){ int v=to[i]; if(v==ff) continue; fa[v]=u; dep[v]=dep[u]+1; dfs1(v,u); } } int find(int x) { if(dep[x]<=kk) return 1; int cnt=1; while(cnt<=kk){ x=fa[x]; cnt++; } return x; } void dfs2(int rt,int u,int ff,int cnt) { if(cnt>kk) return ; vis[u]=1; for(ri i=head[u];i;i=nex[i]){ int v=to[i]; if(v==ff) continue; dfs2(rt,v,u,cnt+1); } } void work() { int ans=0; while(!q.empty()){ int u=q.top().u; q.pop(); if(vis[u]) continue; int k_fa=find(u); dfs2(k_fa,k_fa,0,0); ans++; } printf("%d ",ans); } int main() { freopen("general.in","r",stdin); freopen("general.out","w",stdout); int t; scanf("%d%d%d",&n,&kk,&t); int a,b; for(ri i=1;i<=n-1;++i) scanf("%d%d",&a,&b),add(a,b),add(b,a); if(kk==0) { printf("%d ",n); return 0; } dfs1(1,0); work(); return 0; } /* 4 1 0 1 2 1 3 1 4 8 1 2 1 2 1 3 1 4 1 5 2 6 2 7 3 8 6 1 0 1 2 1 3 1 4 4 5 4 6 16 1 0 1 2 1 3 1 4 2 5 2 6 2 7 3 8 4 9 5 10 10 11 3 12 9 13 11 14 11 15 11 16 */
T3: 星空

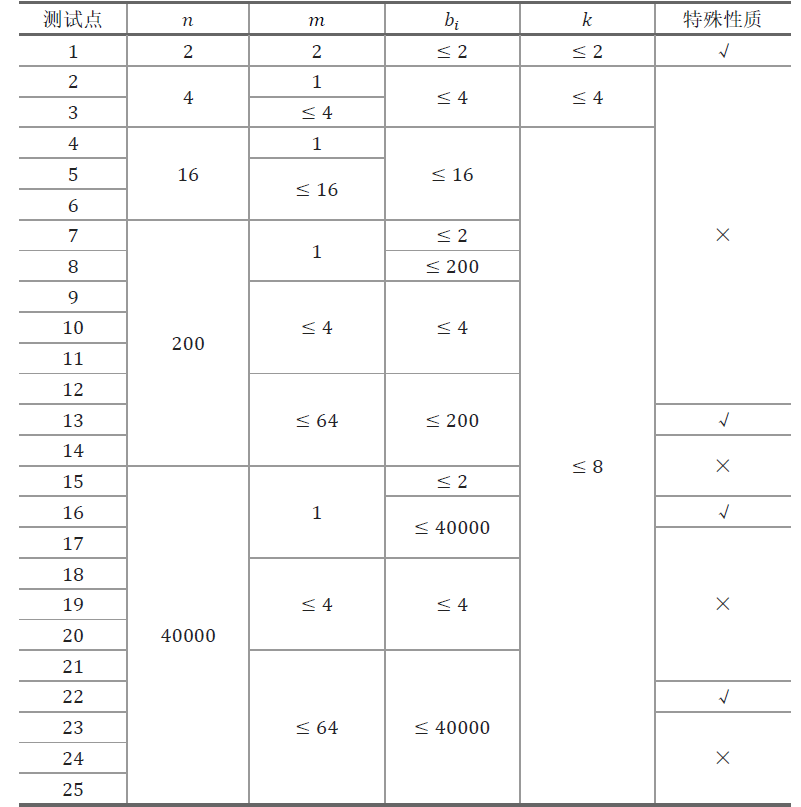
分析:
先将区间修改转换成单点修改,就像差分一样,这里的差分是将相邻的两个异或。
注意开头和结尾默认是1
例如样例:(1)01110(1)
差分后: 11001
然后随便选取一段区间,看区间翻转对应到原序列里是怎么变换的。例如翻转2~4这一段区间:
(1)00000 -> 10000
可以发现,是对l和r+1这两个位置进行了取反。
所以要加入n+1这一个位置!!
最终目标:差分序列为全0(原序列就是全1了)
可以发现,每次翻转一个区间,最多对两个位置的1有贡献。
所以可以将差分序列有1的地方提出来,做一遍bfs,就可以求出每个1和其他1同时被翻转成0所需要的最小步数。
再做一遍状压,求出将所有1翻转成0的贡献即可。
注意:求dis的时候一定要记得memset,因为有可能出现两个1之间不能翻转的情况,此时代价是正无穷。

#include<bits/stdc++.h> using namespace std; #define N 40005 #define ri register int int n,k,m,vis[N],dis[20][N],tot=0,pos[N],s[N],num[N],pre[N],b[N],dp[1<<20]; queue<int> q; void bfs(int u,int *dis)//不能打成 &dis[] { memset(vis,0,sizeof(vis)); dis[u]=0; q.push(u); vis[u]=1; while(!q.empty()){ int x=q.front(); q.pop(); for(ri i=1;i<=m;++i){ int y=x-b[i]; if(y>=1 && !vis[y]) dis[y]=dis[x]+1,q.push(y),vis[y]=1; y=x+b[i]; if(y<=n+1 && !vis[y]) dis[y]=dis[x]+1,q.push(y),vis[y]=1; } } //for(ri i=1;i<=n+1;++i) printf("%d ",dis[i]); //printf(" "); } int main() { //freopen("starlit.in","r",stdin); //freopen("starlit.out","w",stdout); scanf("%d%d%d",&n,&k,&m); for(ri i=0;i<=N-4;++i) s[i]=1;//注意一定要记得把n+1的位置赋成 1 相当于添加了一个位置 操作l~r 变成l~r+1 for(ri i=1;i<=k;++i) scanf("%d",&pos[i]),s[pos[i]]=0; for(ri i=1;i<=m;++i) scanf("%d",&b[i]); for(ri i=1;i<=n+1;++i) pre[i]=s[i]^s[i-1]; memset(dis,0x3f3f3f,sizeof(dis));//一定要memset!! 因为可能两个1之间不能翻转 而不memset的话 翻转的代价会变成 0 for(ri i=1;i<=n+1;++i) if(pre[i]){//for到n+1 num[++tot]=i;//记录1所在的位置 bfs(i,dis[tot]);//求出从这个位置与其他 1同时变成 0 所花费的最小次数 } memset(dp,0x3f3f3f,sizeof(dp)); dp[0]=0; for(ri i=0;i<(1<<tot);++i){ int x=-1; for(ri j=0;j<tot;++j) if(!(i&(1<<j))) { x=j; break; }//找到第一个还没翻转的位置 for(ri j=x+1;j<tot;++j)//枚举第二个还没翻转的位置 if(!( i&(1<<j) )){ int nex=i|(1<<x)|(1<<j); dp[nex]=min(dp[nex],dp[i]+dis[x+1][num[j+1]]); } } printf("%d ",dp[(1<<tot)-1]); return 0; } /* 5 2 2 1 5 3 4 5 2 2 1 2 2 3 */
