题目:

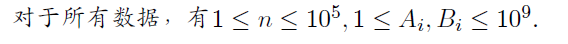
分析:
(这道题是真的难)(声明: 在这位大佬的题解下多做了说明,图片来源也是他的博客。)
首先我们要发现一些小规律:
1.将A和B排序之后并不影响答案
证明:不管哪一列排序放到了哪里,那一列的最大值都应该是Ai。
2.A的最大一定等于B的最大:
很显然,如果不等于,那么最大值放在哪里都不合法。
3.将A和B数组按从小到大的顺序排序后,会变成这种矩形:
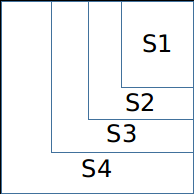
定义f[ i ]为至少有i行不满足,定义至少的原因:两两行之间不会受影响
显然最后我们要求的是恰好有0行不满足,即至少有0行不满足-至少有1行不满足,但因为至少有一行不满足中包含了至少有两行不满足,所以要加上,有加多了至少有三行不满足的情况,以此类推,用容斥原理计算答案。
先推S1的情况,再在S1的基础上得到S2的公式。
公式的解释他写的太好了,这里就不再阐述。

#include<bits/stdc++.h> using namespace std; #define ri register int #define ll long long #define N 100005 const ll mod = 1e9+7; ll a[N],b[N],s[N<<1],invfac[N],fac[N]; int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch<='9'&&ch>='0') x=x*10+ch-'0',ch=getchar(); return fl*x; } ll quick_pow(ll a,ll k) { ll ans=1; while(k) { if(k&1) ans=ans*a%mod; a=a*a%mod; k>>=1; } return ans; } void init(int n) { fac[0]=1; for(ll i=1;i<=n;++i) fac[i]=fac[i-1]*i%mod; invfac[n]=quick_pow(fac[n],mod-2); for(ll i=n;i>=1;--i) invfac[i-1]=invfac[i]*i%mod; } ll C(ll m,ll n) { return fac[n]*invfac[m]%mod *invfac[n-m] %mod; } ll calc(ll a,ll b,ll c,ll d,ll ss) { ll ret=0; for(ll i=0;i<=a;++i){ ll tmp=C(i,a)* quick_pow(( quick_pow(ss,i) * ( quick_pow(ss+1,a+c-i) - quick_pow(ss,a+c-i) +mod) %mod),b) %mod; tmp=tmp * quick_pow(( quick_pow(ss,i) * quick_pow(ss+1,a-i) %mod ),d) %mod; if(i&1) ret=(ret-tmp+mod)%mod; else ret=(ret+tmp)%mod; } return ret; } int main() { freopen("silhouette.in","r",stdin); freopen("silhouette.out","w",stdout); int n=read(),cnt=0; for(ri i=1;i<=n;++i) a[i]=read(),s[++cnt]=a[i]; for(ri i=1;i<=n;++i) b[i]=read(),s[++cnt]=b[i]; sort(a+1,a+1+n); sort(b+1,b+1+n); if(a[n]!=b[n]) { printf("0 "); return 0; } sort(s+1,s+1+cnt); int num=unique(s+1,s+1+2*n)-s-1; int na=n,nb=n,pa=n+1,pb=n+1; init(n); ll ans=1; for(ri i=num;i>=1;--i){ while(na-1 && a[na-1]==s[i]) na--; while(nb-1 && b[nb-1]==s[i]) nb--; ans=ans* calc( pa-na,pb-nb,n-pa+1,n-pb+1,s[i] ) %mod; pa=na; pb=nb; } printf("%lld ",ans); } /* 2 1 2 2 1 */
