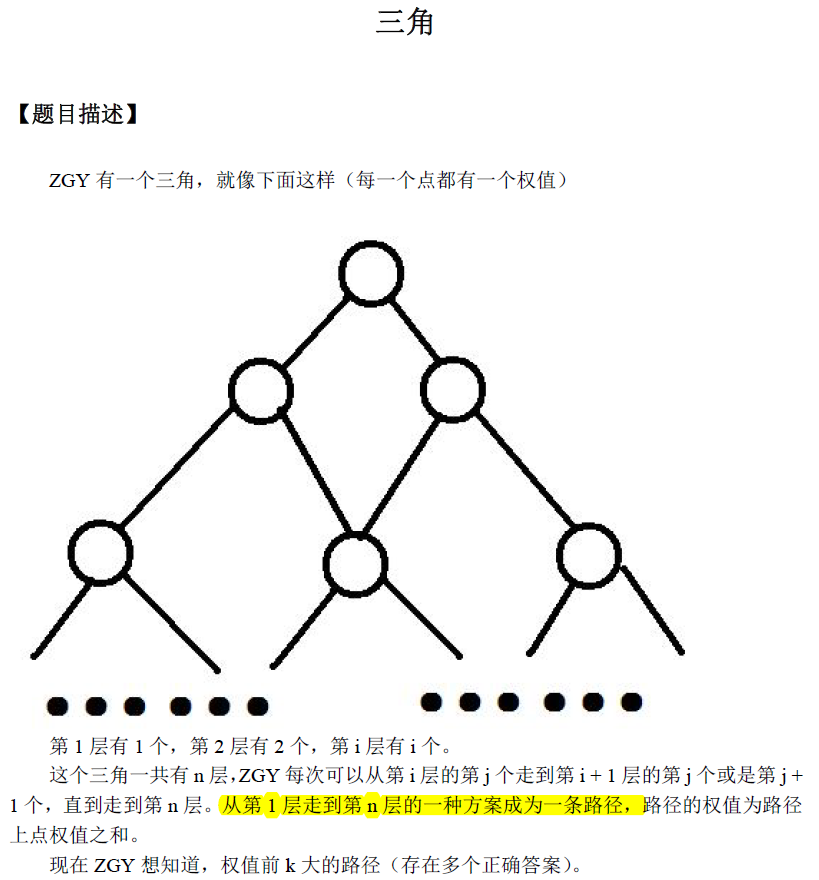
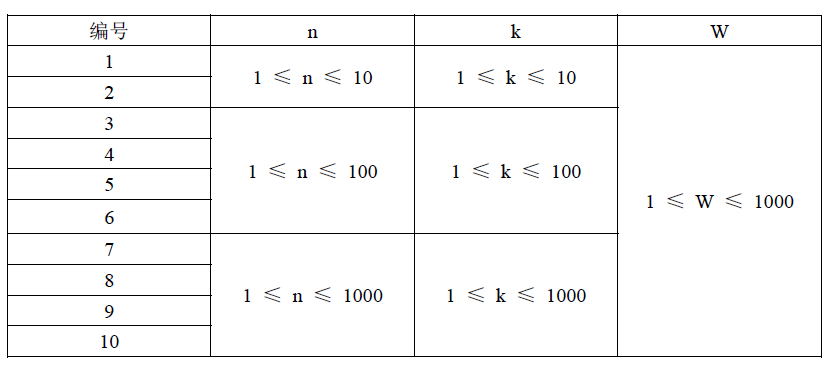
题目:

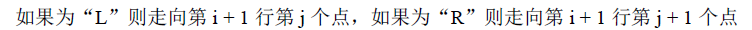
分析:
考虑最暴力的暴搜,怎么才能优化呢?
如果我们确切地知道第k大的路径权值和有多大,那么在dfs里面加一个限制就可以求出所有前k大的路径了。
很显然答案是满足单调性的。
可以二分一个答案,dfs一遍,看满足这个答案的有多少条路径,如果超过k条,就往大的走。
最后把二分出来的答案跑一遍dfs,输出路径即可。
时间复杂度:O(log(n*n)*玄学dfs)

#include<bits/stdc++.h> using namespace std; #define N 1005 #define ri register int int n,k,cnt=0,a[N][N],fl=false,lim,tot,dp[N][N],way[N]; int read() { int x=0,fl=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-') fl=-1; ch=getchar(); } while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return x*fl; } void dfs(int x,int y,int sum) { if(tot>=k) return ; if(sum+dp[x][y]<lim) return ; if(x==n){ tot++; if(fl){ for(ri i=1;i<=n-1;++i) if(way[i]==0) printf("L"); else printf("R"); printf(" "); } return ; } way[x]=0; dfs(x+1,y,sum+a[x][y]); way[x]=1; dfs(x+1,y+1,sum+a[x][y]); } int main() { freopen("tri.in","r",stdin); freopen("tri.out","w",stdout); n=read(); k=read(); for(ri i=1;i<=n;++i) for(ri j=1;j<=i;++j) a[i][j]=read(); for(ri i=1;i<=n;++i) dp[n][i]=a[n][i]; for(ri i=n-1;i>=1;--i) for(ri j=1;j<=i;++j) dp[i][j]=max(a[i][j]+dp[i+1][j],a[i][j]+dp[i+1][j+1]); int l=0,r=1000*1000+1; while(l+1<r){ int mid=(l+r)>>1; lim=mid, tot=0, dfs(1,1,0); if(tot>=k) l=mid; else r=mid; } tot=0; lim=l; fl=true; dfs(1,1,0); } /* 3 3 1 1 100 2 1 1 10 6 1 2 3 4 3 2 3 4 5 6 3 2 4 6 5 7 6 8 4 6 5 3 5 6 3 2 7 4 3 4 5 6 7 3 5 3 2 4 5 6 7 4 6 4 2 2 4 5 6 7 4 6 4 2 4 */
